题目内容
已知 是R上的单调增函数,则
是R上的单调增函数,则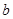 的取值范围是( )
的取值范围是( )
A.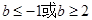 | B.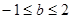 | C.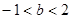 | D.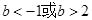 |
B
解析试题分析:先求出函数为递增时b的范围,∵已知 ∴y′=x2+2bx+b+2,∵f(x)是R上的单调增函数,∴x2+2bx+b+2≥0恒成立,∴△≤0,即b2 b 2≤0,则b的取值是1≤b≤2,故选B.
∴y′=x2+2bx+b+2,∵f(x)是R上的单调增函数,∴x2+2bx+b+2≥0恒成立,∴△≤0,即b2 b 2≤0,则b的取值是1≤b≤2,故选B.
考点:函数的单调性与导数的关系..

练习册系列答案
 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案 导学与测试系列答案
导学与测试系列答案
相关题目
函数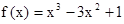 是减函数的区间为 ( )
是减函数的区间为 ( )
A.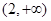 | B.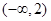 | C.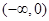 | D.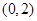 |
若函数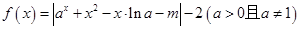 有两个零点,则
有两个零点,则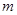 的取值范围( )
的取值范围( )
A.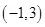 | B.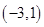 | C.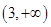 | D.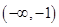 |
已知点P(1,2)是曲线y=2x2上一点,则P处的瞬时变化率为 ( )
| A.2 | B.4 | C.6 | D.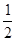 |
曲线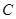 :
: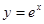 在点
在点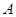 处的切线
处的切线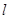 恰好经过坐标原点,则曲线
恰好经过坐标原点,则曲线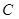 直线
直线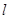 ,
,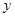 轴围成的图形面积为( )
轴围成的图形面积为( )
A. | B.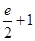 | C.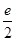 | D.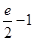 |
函数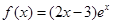 的单调递增区间是( )
的单调递增区间是( )
A.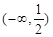 | B.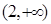 | C. | D.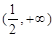 |
函数f(x)=x3+ax2+3x﹣9,已知f(x)在x=﹣3时取得极值,则a=( )
| A.2 | B.3 | C.4 | D.5 |
若曲线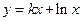 在点
在点 处的切线平行于x轴,则k= ( )
处的切线平行于x轴,则k= ( )
| A.-1 |
| B.1 |
| C.-2 |
| D.2 |
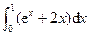 =( )
=( )
| A.1 |
B.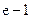 |
| C.e |
| D.1+e |