题目内容
已知椭圆 :
: 的离心率为
的离心率为 ,右焦点为(
,右焦点为( ,0).
,0).
(1)求椭圆 的方程;
的方程;
(2)若过原点 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于 ,
, 两点,求证:点
两点,求证:点 到直线
到直线 的距离为定值.
的距离为定值.
 :
: 的离心率为
的离心率为 ,右焦点为(
,右焦点为( ,0).
,0).(1)求椭圆
 的方程;
的方程; (2)若过原点
 作两条互相垂直的射线,与椭圆交于
作两条互相垂直的射线,与椭圆交于 ,
, 两点,求证:点
两点,求证:点 到直线
到直线 的距离为定值.
的距离为定值.(1)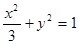 (2)见解析
(2)见解析
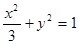 (2)见解析
(2)见解析试题分析:(1)由离心率
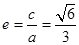 ,右焦点坐标易得各常量值. (2)先假设
,右焦点坐标易得各常量值. (2)先假设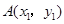
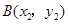 ,当直线AB斜率存在时,与椭圆方程联立,可得
,当直线AB斜率存在时,与椭圆方程联立,可得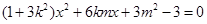 又OA⊥OB,满足
又OA⊥OB,满足 根与系数的关系,可得4 m2=3 k2+3,代入点
根与系数的关系,可得4 m2=3 k2+3,代入点 到直线
到直线 的距离可得d=
的距离可得d=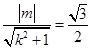 .
.试题解析:(1)由右焦点为(
 ,0),则
,0),则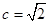 ,又
,又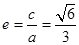 ,所以
,所以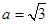 ,
,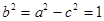
那么
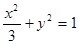 4分
4分 (2) 设
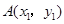 ,
,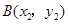 ,若k存在,则设直线AB:y=kx+m.
,若k存在,则设直线AB:y=kx+m.由
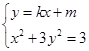 ,得
,得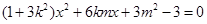 6分
6分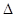 >0,
>0,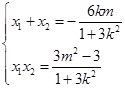 8分
8分有OA⊥OB知x1x2+y1y2=x1x2+(k x1+m) (k x2+m)=(1+k2) x1x2+k m(x1+x2)=0 10分
代入,得4 m2=3 k2+3原点到直线AB的距离d=
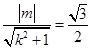 . 12分
. 12分当AB的斜率不存在时,
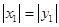 ,可得
,可得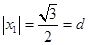 ,依然成立. 13分
,依然成立. 13分所以点O到直线
 的距离为定值
的距离为定值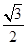 14分
14分
练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
 (a>b>0)的离心率为
(a>b>0)的离心率为 ,且过点(
,且过点( ).
). (1<R<2)相切于点A,且l与椭圆E只有一个公共点B.
(1<R<2)相切于点A,且l与椭圆E只有一个公共点B. ;
; 取得最大值?并求出最大值.
取得最大值?并求出最大值.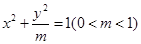 的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
的左顶点为A,M是椭圆C上异于点A的任意一点,点P与点A关于点M对称.
 ,求m的值;
,求m的值; ,求m的取值范围.
,求m的取值范围.
 的左、右焦点分别
的左、右焦点分别 、
、 ,点
,点 是椭圆短轴的一个端点,且焦距为6,
是椭圆短轴的一个端点,且焦距为6,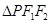 的周长为16.
的周长为16.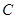 的方程;
的方程;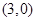 且斜率为
且斜率为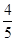 的直线
的直线 被椭圆
被椭圆 经过点
经过点 ,一个焦点为
,一个焦点为 .
. 的方程;
的方程; 与
与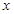 轴交于点
轴交于点 ,与椭圆
,与椭圆 两点,线段
两点,线段 的垂直平分线与
的垂直平分线与 ,求
,求 的取值范围.
的取值范围. 是离心率为
是离心率为 的椭圆
的椭圆 :
:
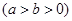 上的一点,斜率为
上的一点,斜率为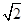 的直线
的直线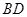 交椭圆
交椭圆 ,
, 两点,且
两点,且 、
、
 ,
, 的斜率之和为定值.
的斜率之和为定值. =1(a>b>0),双曲线
=1(a>b>0),双曲线 =1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
=1的两条渐近线为l1、l2,过椭圆C的右焦点F作直线l,使l⊥l1.又l与l2交于P点,设l与椭圆C的两个交点由上至下依次为A、B(如图).
 =λ
=λ ,求λ的最大值.
,求λ的最大值. =1(a>b>0),称圆心在原点O、半径是
=1(a>b>0),称圆心在原点O、半径是 的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F(
的圆为椭圆C的“准圆”.已知椭圆C的一个焦点为F( ,0),其短轴的一个端点到点F的距离为
,0),其短轴的一个端点到点F的距离为 .
. ·
· 的取值范围;
的取值范围; =1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A=
=1(a>b>0)的左、右焦点,A、B分别是此椭圆的右顶点和上顶点,P是椭圆上一点,O是坐标原点,OP∥AB,PF1⊥x轴,F1A= +
+ ,则此椭圆的方程是________________.
,则此椭圆的方程是________________.