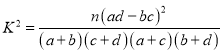题目内容
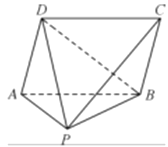
【题目】如图,在四棱锥![]() 中,四边形
中,四边形![]() 为平行四边形,
为平行四边形,![]() 为直角三角形且
为直角三角形且![]() ,
,![]() 是等边三角形.
是等边三角形.
(1)求证:![]() ;
;
(2)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
【答案】(1)见解析; (2)![]() .
.
【解析】
(1)取AP中点F,连接DM,BM,由已知可证PA⊥DM,PA⊥BM,又DM∩BM=M,可得PA⊥平面DMB,因为BD平面DMB,可证PA⊥BD;
(2)由已知可得△DAP是等腰三角形,又△ABP是等边三角形,可求出MD⊥MB,以MP,MB,MD所在直线分别为x,y,z轴建立空间直角坐标系.求出平面DPC与平面PCB的一个法向量,由两法向量所成角的余弦值得二面角D﹣PC﹣B的余弦值,进一步求得正弦值.
(1)证明:取![]() 中点
中点![]() ,连
,连![]() ,
,
∵![]() ,
,![]() 为等边三角形,
为等边三角形,
∴![]() ,又
,又![]() ,
,
∴![]() 平面
平面![]() ,又∵
,又∵![]() 平面
平面![]() ,∴
,∴![]() .
.
(2)解:∵![]() ,
,![]() 为
为![]() 中点,结合题设条件可得
中点,结合题设条件可得![]() ,
,
∴![]() ,∴
,∴![]() .
.
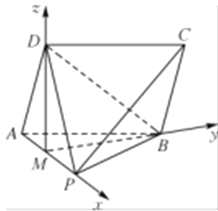
如图,以![]() 所在直线分别为
所在直线分别为![]() 轴建立空间直角坐标系,
轴建立空间直角坐标系,
则![]() ,
,
得![]() ,
,![]() ,
,![]() ,
,![]()
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则 即
即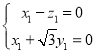 ,∴
,∴![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
由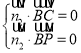 即
即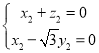 ,∴
,∴![]() .
.
∴![]()
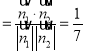 .
.
设二面角![]() 的平面角为
的平面角为![]() ,则由图可知
,则由图可知![]() ,∴
,∴![]() .
.

练习册系列答案
相关题目
【题目】某校抽取了100名学生期中考试的英语和数学成绩,已知成绩都不低于100分,其中英语成绩的频率分布直方图如图所示,成绩分组区间是![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
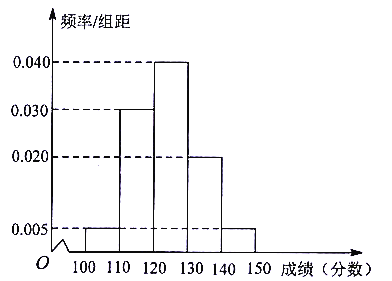
(1)根据频率分布直方图,估计这100名学生英语成绩的平均数和中位数(同一组数据用该区间的中点值作代表);
(2)若这100名学生数学成绩分数段的人数y的情况如下表所示:
分组区间 |
|
|
|
|
|
y | 15 | 40 | 40 | m | n |
且区间![]() 内英语人数与数学人数之比为
内英语人数与数学人数之比为![]() ,现从数学成绩在
,现从数学成绩在![]() 的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在
的学生中随机选取2人,求选出的2人中恰好有1人数学成绩在![]() 的概率.
的概率.