题目内容
已知双曲线![]() 的右焦点为F,过点F的动直线与双曲线相交与A、B两点,点C的坐标是(1,0).
的右焦点为F,过点F的动直线与双曲线相交与A、B两点,点C的坐标是(1,0).
(I)证明![]() 为常数;
为常数;
(Ⅱ)若动点![]() (其中
(其中![]() 为坐标原点),求点
为坐标原点),求点![]() 的轨迹方程.
的轨迹方程.
解:由条件知![]() ,设
,设![]() ,
,![]() .
.
(I)当![]() 与
与![]() 轴垂直时,可设点
轴垂直时,可设点![]() 的坐标分别为
的坐标分别为![]() ,
,![]() ,
,
此时![]() =(1,
=(1,![]() )?(1,-
)?(1,-![]() )=-1
)=-1
当![]() 不与
不与![]() 轴垂直时,设直线
轴垂直时,设直线![]() 的方程是
的方程是![]() .
.
代入![]() ,有
,有![]() .
.
则![]() 是上述方程的两个实根,所以
是上述方程的两个实根,所以![]() ,
,![]() ,
,
于是![]() =
=![]()
![]()
![]()
![]() .
.
综上所述,![]() 为常数
为常数![]() .
.
(II)解法一:设![]() ,则
,则![]() ,
,![]() ,
,
![]() ,
,![]() ,由
,由![]() 得:
得:
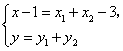 即
即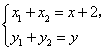
于是![]() 的中点坐标为
的中点坐标为![]() .
.
当![]() 不与
不与![]() 轴垂直时,
轴垂直时,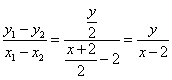 ,即
,即![]() .
.
又因为![]() 两点在双曲线上,所以
两点在双曲线上,所以![]() ,
,![]() ,两式相减得
,两式相减得
![]() ,即
,即![]() .
.
将![]() 代入上式,化简得
代入上式,化简得![]() .
.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,求得
,求得![]() ,也满足上述方程.
,也满足上述方程.
所以点![]() 的轨迹方程是
的轨迹方程是![]() .
.
解法二:同解法一得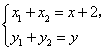 ……………………………………①
……………………………………①
当![]() 不与
不与![]() 轴垂直时,由(I) 有
轴垂直时,由(I) 有![]() .…………………②
.…………………②
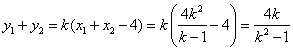 .………………………③
.………………………③
由①②③得![]() .…………………………………………………④
.…………………………………………………④
![]() .……………………………………………………………………⑤
.……………………………………………………………………⑤
当![]() 时,
时,![]() ,由④⑤得,
,由④⑤得,![]() ,将其代入⑤有
,将其代入⑤有
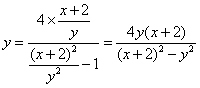 .整理得
.整理得![]() .
.
当![]() 时,点
时,点![]() 的坐标为
的坐标为![]() ,满足上述方程.
,满足上述方程.
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() ,求得
,求得![]() ,也满足上述方程.
,也满足上述方程.
故点![]() 的轨迹方程是
的轨迹方程是![]() .
.

练习册系列答案
 夺冠训练单元期末冲刺100分系列答案
夺冠训练单元期末冲刺100分系列答案 新思维小冠军100分作业本系列答案
新思维小冠军100分作业本系列答案 名师指导一卷通系列答案
名师指导一卷通系列答案
相关题目