题目内容
下列结论:①当a为任意实数时,直线(a-1)x-y+2a+1=0恒过定点P,则过点P且焦点在y轴上的抛物线的标准方程是x2=
| 4 |
| 3 |
②已知双曲线的右焦点为(5,0),一条渐近线方程为2x-y=0,则双曲线的标准方程是
| x2 |
| 5 |
| y2 |
| 20 |
③抛物线y=ax2(a≠0)的准线方程为y=-
| 1 |
| 4a |
④已知双曲线
| x2 |
| 4 |
| y2 |
| m |
其中所有正确结论的个数是
分析:①中求出符合条件的抛物线方程,判断得①正确;②中根据渐近线方程求得a和b的关系进而根据焦距求得a和b,椭圆方程可得.判断②正确;③把抛物线方程整理成标准方程,进而根据抛物线的性质可得抛物线的准线方程,判断③正确.④根据离心率的范围求得-12<m<0判断④正确.
解答:解:①整理直线方程得(x+2)a+(1-x-y)=0,可知直线过定点(-2,3),符合条件的方程是x2=
y,则①正确
②依题意知
=2,a2+b2=25求得a=
,b=2
,故可知结论②正确.
③整理抛物线方程得x2=
y,根据抛物线性质可知准线方程为y=-
故③正确.
④离心率1<e=
<2,解得-12<m<0,又m<0,,故m的范围是-12<m<0,④正确,
故正确结论数为4
故答案为4
| 4 |
| 3 |
②依题意知
| b |
| a |
| 5 |
| 5 |
③整理抛物线方程得x2=
| 1 |
| a |
| 1 |
| 4a |
④离心率1<e=
| ||
| 2 |
故正确结论数为4
故答案为4
点评:本题主要考查了圆锥曲线的基本性质.熟练掌握圆锥曲线的性质是正确解题的基础.

练习册系列答案
相关题目
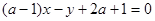 恒过定点P,则过点P且焦点在y轴上的抛物线的标准方程是
恒过定点P,则过点P且焦点在y轴上的抛物线的标准方程是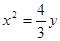 ;
;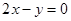 ,则双曲线的标准方程是
,则双曲线的标准方程是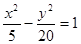 ;
;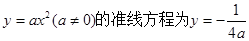 ;
;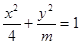 ,其离心率
,其离心率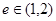 ,则m的取值范围是(-12,0)。
,则m的取值范围是(-12,0)。 ;
; ;
; ;
; ,其离心率e∈(1,2),则m的取值范围是(-12,0).
,其离心率e∈(1,2),则m的取值范围是(-12,0).