题目内容
10.(1)已知关于x的不等式ax2+2x+c>0的解集为(-$\frac{1}{3}$,$\frac{1}{2}$),求a+c的值;(2)已知实数x,y满足不等式组$\left\{\begin{array}{l}{2x-y≥0}\\{x+2y≥0}\\{3x+y-5≤0}\end{array}\right.$ 求2x+y的最大值.
分析 (1)根据不等式的解集和一元二次方程根的关系即可求解a+c的值;
(2)利用线性规划的知识结合目标函数的几何意义进行求解即可.
解答 解:(1)由ax2+2x+c>0的解集为(-$\frac{1}{3}$,$\frac{1}{2}$)知a<0,且-$\frac{1}{3}$,$\frac{1}{2}$为方程ax2+2x+c=0的两个根,
由根与系数的关系得-$\frac{1}{3}$+$\frac{1}{2}$=-$\frac{2}{a}$,-$\frac{1}{3}$×$\frac{1}{2}$=$\frac{c}{a}$,
解得a=-12,c=2,
∴a+c=-10.
(2)设z=2x+y,得y=-2x+z,作出不等式对应的区域,
平移直线y=-2x+z,由图象可知当直线经过点B时,直线的截距最大,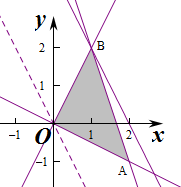
由$\left\{\begin{array}{l}{2x-y=0}\\{3x+y-5=0}\end{array}\right.$,解得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
即B(1,2),代入z=2x+y,得z=2x+y=4.
点评 本题主要考查线性规划以及一元二次不等式的应用,利用目标函数的几何意义,结合数形结合的数学思想是解决此类问题的基本方法.

练习册系列答案
 特高级教师点拨系列答案
特高级教师点拨系列答案
相关题目
18.正项等比数列{an}中的a1,a9是函数f(x)=$\frac{1}{3}{x^3}-a{x^2}$+x+1的极值点,则lna5=( )
| A. | -1 | B. | 0 | C. | 1 | D. | 与a的值有关 |
15.设△ABC的内角A、B、C所对的边分别为a,b,c,若bcosC+ccosB=asinA,则△ABC的形状为( )
| A. | 锐角三角形 | B. | 钝角三角形 | C. | 直角三角形 | D. | 等腰直角三角形 |
2.复平面上表示复数z=1-i(i为虚数单位)的点在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
19.抛物线x2=2y的焦点到准线的距离是( )
| A. | 2 | B. | 1 | C. | $\frac{1}{4}$ | D. | $\frac{1}{8}$ |