题目内容
已知函数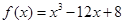 在区间
在区间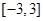 上的最大值与最小值分别为
上的最大值与最小值分别为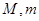 ,则
,则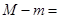 ___________.
___________.
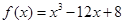 在区间
在区间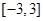 上的最大值与最小值分别为
上的最大值与最小值分别为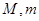 ,则
,则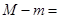 ___________.
___________.32
试题分析:解:∵函数f(x)=x3-12x+8,∴f′(x)=3x2-12,令f′(x)>0,解得x>2或x<-2;令f′(x)<0,解得-2<x<2,故函数在[-2,2]上是减函数,在[-3,-2],[2,3]上是增函数,所以函数在x=2时取到最小值f(2)=8-24+8=-8,在x=-2时取到最大值f(-2)=-8+24+8=24,即M=24,m=-8,∴M-m=32,故填写32.
点评:本题重点考查导数知识的运用,考查函数的最值、单调性,解答本题关键是研究出函数的单调性,利用函数的单调性确定出函数的最值

练习册系列答案
相关题目
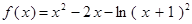 .
.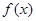 的单调递增区间;
的单调递增区间;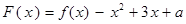 在
在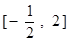 上只有一个零点,求实数
上只有一个零点,求实数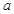 的取值范围.
的取值范围. 在R上可导,且
在R上可导,且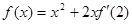 ,则
,则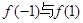 的大小关系是( )
的大小关系是( )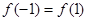
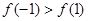
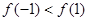
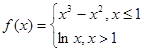 .
.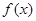 的单调递减区间;
的单调递减区间;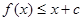 对一切
对一切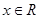 恒成立,求
恒成立,求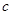 的取值范围.
的取值范围. 在
在 处取极值,则
处取极值,则 .
.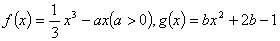 .
.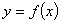 与曲线
与曲线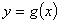 在它们的交点
在它们的交点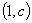 处具有公共切线,求
处具有公共切线,求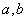 的值;
的值;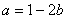 时,若函数
时,若函数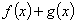 在区间
在区间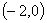 内恰有两个零点,求
内恰有两个零点,求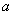 的取值范围;
的取值范围;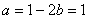 时,求函数
时,求函数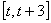 上的最大值
上的最大值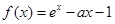 (
(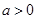 ,
,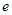 为自然对数的底数).
为自然对数的底数).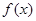 的最小值;
的最小值;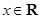 恒成立,求实数
恒成立,求实数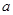 的值;
的值;
 满足0<
满足0<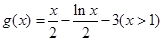 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;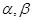 ,
,