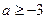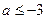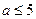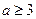题目内容
.已知函数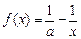
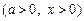 .
.
(1)求证: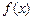 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;
(2)若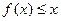 在(0,+∞)上恒成立,求
在(0,+∞)上恒成立,求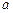 的取值范围。
的取值范围。
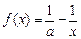
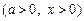 .
. (1)求证:
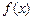 在(0,+∞)上是增函数;
在(0,+∞)上是增函数;(2)若
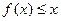 在(0,+∞)上恒成立,求
在(0,+∞)上恒成立,求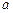 的取值范围。
的取值范围。(1)证明 任取
任取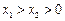
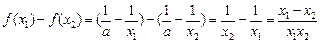 4分
4分
∵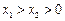 ,∴
,∴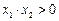 ,
,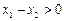 ,
,
∴
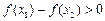 , 6分
, 6分
即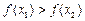 ,故
,故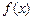 在(0,+∞)上是增函数. 7分
在(0,+∞)上是增函数. 7分
(2)解: ∵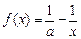 在(0,+∞)上恒成立,且a>0,
在(0,+∞)上恒成立,且a>0,
∴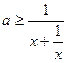 在(0,+∞)上恒成立, 9分
在(0,+∞)上恒成立, 9分
令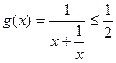 ,当且仅当
,当且仅当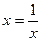 即x=1时取等号 11分
即x=1时取等号 11分
要使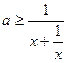 在(0,+∞)上恒成立,则
在(0,+∞)上恒成立,则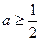
 14分
14分
故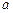 的取值范围是[
的取值范围是[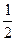 ,+∞). 15分
,+∞). 15分
 任取
任取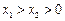
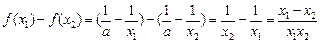 4分
4分∵
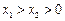 ,∴
,∴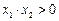 ,
,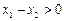 ,
,∴

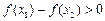 , 6分
, 6分即
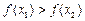 ,故
,故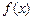 在(0,+∞)上是增函数. 7分
在(0,+∞)上是增函数. 7分 (2)解: ∵
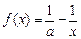 在(0,+∞)上恒成立,且a>0,
在(0,+∞)上恒成立,且a>0,∴
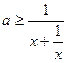 在(0,+∞)上恒成立, 9分
在(0,+∞)上恒成立, 9分令
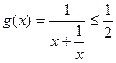 ,当且仅当
,当且仅当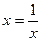 即x=1时取等号 11分
即x=1时取等号 11分要使
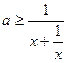 在(0,+∞)上恒成立,则
在(0,+∞)上恒成立,则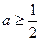
 14分
14分故
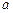 的取值范围是[
的取值范围是[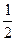 ,+∞). 15分
,+∞). 15分略

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
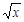
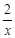
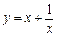 在
在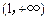 上为增函数.
上为增函数. (升)关于行驶速度x(千米/小时)的函数解析式可以表示为:
(升)关于行驶速度x(千米/小时)的函数解析式可以表示为: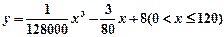 已知甲、乙两地相距100千米。
已知甲、乙两地相距100千米。 速行驶时,从甲地到乙地要耗油多少升?
速行驶时,从甲地到乙地要耗油多少升?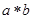 为:
为: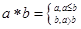 如
如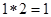 ,则函数
,则函数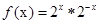 的值域为
的值域为 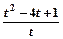 的最小值为________.
的最小值为________.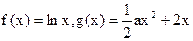 ,若
,若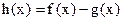 存在单调减区间,则实数
存在单调减区间,则实数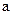 的取值范围是( )
的取值范围是( )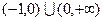
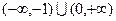
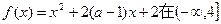 上是递减的,则
上是递减的,则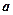 的取值范围是( )
的取值范围是( )