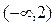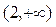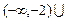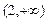题目内容
已知y＝loga(2－ax)在[0,1]上是x的减函数，则a的取值范围是( )
| A．(0,1) | B．(1,2) |
| C．(0,2) | D．[2，＋∞) |
B
先将复合函数的结构剖析出来，是由t=2-ax，y=logat复合而成．再分别分析两个简单函数的单调性，根据复合函数法则判断．
解：原函数是由简单函数t=2-ax和y=logat共同复合而成．
∵a＞0，∴t=2-ax为定义域上减函数，
而由复合函数法则和题意得到，
y=logat在定义域上为增函数，∴a＞1
又函数t=2-ax＞0在（-1，1）上恒成立，则2-a>0即可．
∴a<2．
综上，1＜a<2，
故答案为B．
解：原函数是由简单函数t=2-ax和y=logat共同复合而成．
∵a＞0，∴t=2-ax为定义域上减函数，
而由复合函数法则和题意得到，
y=logat在定义域上为增函数，∴a＞1
又函数t=2-ax＞0在（-1，1）上恒成立，则2-a>0即可．
∴a<2．
综上，1＜a<2，
故答案为B．
练习册系列答案
通城学典默写能手系列答案
相关题目
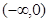的是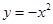
. 
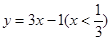
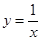
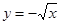
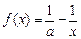
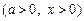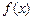在(0,+∞)上是增函数；
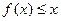在(0,+∞)上恒成立，求
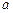的取值范围。
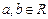，记max｛a,b｝=
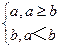函数f（x）＝max｛|x+1|,|x-2|｝(x
R)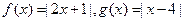
。（1）求不等式
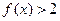的解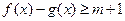
的解集为R,求实数m的取值范围。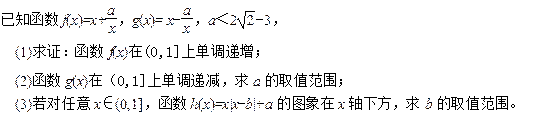
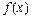是定义在R上的偶函数，在
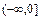上是减函数，且
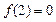则使
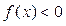的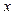
的取值范围是
