Question

【题目】已知椭圆C：，直线l：y＝kx+b与椭圆C相交于A、B两点．

（1）如果k+b＝﹣，求动直线l所过的定点；

（2）记椭圆C的上顶点为D，如果∠ADB＝，证明动直线l过定点P（0，﹣）；

（3）如果b＝﹣，点B关于y轴的对称点为B，向直线AB是过定点？如果是，求出定点的坐标；如果不是，请说明理由．

Answer 1

【答案】（1）定点（1，﹣）；（2）见解析；（3）定点（0，﹣2）．

【解析】

（1）把b＝﹣k﹣代入直线方程可得定点坐标；

（2）根据∠ADB＝，可得,结合韦达定理可得关系；

（3）结合对称性求出直线AB的方程，结合韦达定理，从而可得定点坐标.

（1）∵k+b＝﹣，∴b＝﹣k﹣，∴y＝kx﹣k﹣＝k（x﹣1）﹣，

所以动直线l过定点（1，﹣）．

（2）联立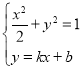消去y得（1+2k2）x2+4kbx+2b2﹣2＝0，

设A（x1，y1），B（x2，y2），则x1+x2＝﹣ ，

∵∠ADB＝，又D（0，1），

∴（x1，y1﹣1）（x2，y2﹣1）＝x1x2+（y1﹣1）（y2﹣1）＝x1x2+（kx1+b﹣1）（kx2+b﹣1）

＝x1x2+k2x1x2+（b﹣1）2+k（b﹣1）（x1+x2）

＝（1+k2）x1x2+k（b﹣1）（x1+x2）+（b﹣1）2

＝（1+k2）×+k（b﹣1）×+（b﹣1）2

＝（b﹣1），

∴（b﹣1）＝0，又b≠1（否则直线l过D），

∴b＝﹣，所以动直线l过定点（0，﹣）.

（3）b＝﹣，直线l为：y＝kx﹣，由（2）知x1+x2＝，

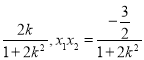经过A（x1，y1），B′（﹣x2，y2）的直线方程为： ，

∴ ，

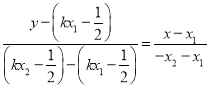令x＝0得y﹣ ，

∴y＝kx1﹣ ，

所以直线AB′是过定点（0，﹣2）．