题目内容
【题目】设Sn为数列{an}的前n项和,若an>0,a1=1,且2Sn=an(an+t)(t∈R,n∈N*),则S100=_____.
【答案】5050
【解析】
先由题设条件求出t,再由2Sn=an(an+1)得2Sn﹣1=an﹣1(an﹣1+1),进而得出Sn,代入求S100.
∵an>0,a1=1,且2Sn=an(an+t)(t∈R,n∈N*),
∴当n=1,有2S1=a1(a1+t),即2=1+t,
解得:t=1.
∴2Sn=an(an+1)①,
又当n≥2时,有2Sn﹣1=an﹣1(an﹣1+1)②,
∴①﹣②可得:2(Sn﹣Sn﹣1)=an(an+1)﹣an﹣1(an﹣1+1),
整理得:an+an﹣1=an2﹣an﹣12,
∵an>0,
∴an﹣an﹣1=1.
所以数列{an}是以a1=1为首项,公差d=1的等差数列,
∴其前n项和Sn![]() ,
,
∴S100![]() 5050.
5050.
故答案为:5050.

 小夫子全能检测系列答案
小夫子全能检测系列答案【题目】水稻是人类重要的粮食作物之一,耕种与食用的历史都相当悠久,日前我国南方农户在播种水稻时一般有直播、撒酒两种方式.为比较在两种不同的播种方式下水稻产量的区别,某市红旗农场于2019年选取了200块农田,分成两组,每组100块,进行试验.其中第一组采用直播的方式进行播种,第二组采用撒播的方式进行播种.得到数据如下表:
产量(单位:斤) 播种方式 | [840,860) | [860,880) | [880,900) | [900,920) | [920,940) |
直播 | 4 | 8 | 18 | 39 | 31 |
散播 | 9 | 19 | 22 | 32 | 18 |
约定亩产超过900斤(含900斤)为“产量高”,否则为“产量低”
(1)请根据以上统计数据估计100块直播农田的平均产量(同一组中的数据用该组区间的中点值为代表)
(2)请根据以上统计数据填写下面的2×2列联表,并判断是否有99%的把握认为“产量高”与“播种方式”有关?
产量高 | 产量低 | 合计 | |
直播 | |||
散播 | |||
合计 |
附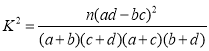 :
:
P(K2≥k0) | 0.10 | 0.010 | 0.001 |
k0 | 2.706 | 6.635 | 10.828 |

