题目内容
如图,在平面直角坐标系 中,点A(0,3),直线
中,点A(0,3),直线 :
: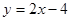 ,设圆
,设圆 的半径为1,圆心在
的半径为1,圆心在 上.
上.
(1)若圆心 也在直线
也在直线 上,过点A作圆
上,过点A作圆 的切线,求切线的方程;
的切线,求切线的方程;
(2)若圆 上存在点
上存在点 ,使
,使 ,求圆心
,求圆心 的横坐标
的横坐标 的取值范围.
的取值范围.
(1)切线方程为 和
和 ;(2)
;(2) .
.
解析试题分析:(1)先联立直线方程求出圆心坐标,写出圆的方程,设出直线方程,利用圆心到此直线距离为半径求解;(2)设出 点坐标,利用
点坐标,利用 可得
可得 ,在
,在 上,又
上,又 在圆
在圆 上,利用两圆相交建立关系求解.
上,利用两圆相交建立关系求解.
试题解析:(1)联立 和
和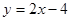 可得圆心
可得圆心 (3,2),又因为半径为1,
(3,2),又因为半径为1,
所以圆 的方程为
的方程为
设过点A的切线方程为:
圆心到直线的距离为
所以 或
或
所求切线方程为 和
和 .
.
(2)设点 ,因为
,因为
所以

又因为点 在圆
在圆 上,
上,
所以圆 与圆
与圆 相交,
相交,
设点 ,两圆圆心距满足:
,两圆圆心距满足: , 所以
, 所以 .
.
考点:直线和圆的位置关系、圆与圆的位置关系、点到线的距离公式.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 与圆的位置关系。
与圆的位置关系。 中,点
中,点 ,直线
,直线 。设圆
。设圆 的半径为
的半径为 ,圆心在
,圆心在 上。
上。
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围。
的取值范围。 外切于点
外切于点 ,且半径为
,且半径为 的圆的方程.
的圆的方程. 是抛物线
是抛物线 上的点,
上的点, 是
是 的焦点, 以
的焦点, 以 为直径的圆
为直径的圆 与
与 轴的另一个交点为
轴的另一个交点为 .
. 且斜率大于零的直线
且斜率大于零的直线 与抛物线
与抛物线 两点,
两点, 为坐标原点,
为坐标原点, 的面积为
的面积为 ,证明:直线
,证明:直线 ,
, 过定点
过定点 (1,0),且与圆
(1,0),且与圆 相切,求
相切,求 的半径为3,圆心在直线
的半径为3,圆心在直线 :
: 上,且与圆
上,且与圆 中,点
中,点 ,直线
,直线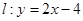 ,设圆
,设圆 的半径为1, 圆心在
的半径为1, 圆心在 上.
上.
 上,过点
上,过点 作圆
作圆 ,使
,使 ,求圆心
,求圆心 的取值范围.
的取值范围. ,直线
,直线 :
: .
. 时,求直线
时,求直线