题目内容
【题目】椭圆![]() 上动点
上动点![]() 到两个焦点的距离之和为4,且到右焦点距离的最大值为
到两个焦点的距离之和为4,且到右焦点距离的最大值为![]() .
.
(1)求椭圆![]() 的方程;
的方程;
(2)设点![]() 为椭圆的上顶点,若直线
为椭圆的上顶点,若直线![]() 与椭圆
与椭圆![]() 交于两点
交于两点![]() (
(![]() 不是上下顶点)
不是上下顶点)![]() .试问:直线
.试问:直线![]() 是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;
是否经过某一定点,若是,求出该定点的坐标;若不是,请说明理由;
(3)在(2)的条件下,求![]() 面积的最大值.
面积的最大值.
【答案】(1)![]() ;(2)
;(2)![]() ;(3)见解析
;(3)见解析
【解析】
(1)先根据已知得到a,c的值,再求b的值,即得椭圆的方程.(2) 设直线![]() (k必存在),
(k必存在),![]() ,联立直线和椭圆的方程得到韦达定理,再利用韦达定理化简
,联立直线和椭圆的方程得到韦达定理,再利用韦达定理化简![]() 得到
得到![]() ,再求出直线l所经过的定点.(3)先求出
,再求出直线l所经过的定点.(3)先求出![]() ,再换元利用基本不等式求面积的最大值.
,再换元利用基本不等式求面积的最大值.
(1)由已知得:2a=4∴a=2,,![]() ,b=1,∴方程为:
,b=1,∴方程为:![]() .
.
(2)依题意可设直线![]() (k必存在),
(k必存在),![]() ,将
,将![]() 代入椭圆方程得
代入椭圆方程得![]() .
.![]() ,
,![]() ∵
∵
![]() ∴
∴![]()
∴![]()
![]() ,
,
∵点B为椭圆的上顶点,且![]() ,
,
∴![]() ,
,
![]() ,
,![]() 或
或![]() (舍去),∴直线l
(舍去),∴直线l![]() 必过定点
必过定点![]()
(3)不难得到:![]() ,
,
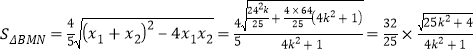 ,
,
令![]() ,则
,则![]() ,
,
∴![]() (当
(当![]() ,即
,即![]() 时取等号).
时取等号).

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案【题目】第31届夏季奥林匹克运动会于2016年8月5日至8月21日在巴西里约热内卢举行.如表是近五届奥运会中国代表团和俄罗斯代表团获得的金牌数的统计数据(单位:枚).
第30届伦敦 | 第29届北京 | 第28届雅典 | 第27届悉尼 | 第26届亚特兰大 | |
中国 | 38 | 51 | 32 | 28 | 16 |
俄罗斯 | 24 | 23 | 27 | 32 | 26 |
(1)根据表格中两组数据在答题卡上完成近五届奥运会两国代表团获得的金牌数的茎叶图,并通过茎叶图比较两国代表团获得的金牌数的平均值及分散程度(不要求计算出具体数值,给出结论即可);
(2)如表是近五届奥运会中国代表团获得的金牌数之和![]() (从第26届算起,不包括之前已获得的金牌数)随时间
(从第26届算起,不包括之前已获得的金牌数)随时间![]() 变化的数据:
变化的数据:
时间 | 26 | 27 | 28 | 29 | 30 |
金牌数之和 | 16 | 44 | 76 | 127 | 165 |
作出散点图如图:

由图可以看出,金牌数之和![]() 与时间
与时间![]() 之间存在线性相关关系,请求出
之间存在线性相关关系,请求出![]() 关于
关于![]() 的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?
的线性回归方程,并预测到第32届奥运会时中国代表团获得的金牌数之和为多少?


