题目内容
(本小题满分12分)
将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体
(Ⅰ)从这些小正方体中任取1个,求其中至少有两面涂有颜色的概率;
(Ⅱ)从中任取2个小正方体,求2个小正方体涂上颜色的面数之和为4的概率。
将一个各个面上均涂有颜色的正方体锯成27个同样大小的小正方体
(Ⅰ)从这些小正方体中任取1个,求其中至少有两面涂有颜色的概率;
(Ⅱ)从中任取2个小正方体,求2个小正方体涂上颜色的面数之和为4的概率。
解:依题意可知,锯成的27个小正方体中,有三面有色的有8个,二面有色的有12个 ,一面有色的有6个,没有色的有1个。………………3分
,一面有色的有6个,没有色的有1个。………………3分
(Ⅰ) 从这些小正方体中任取1个,含有面数为
从这些小正方体中任取1个,含有面数为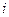 的事件为
的事件为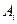 (
(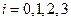 ),则其中至少有两面涂颜色的概率P=
),则其中至少有两面涂颜色的概率P= ;……………………6分
;……………………6分
(Ⅱ)根据题意,设从中任取2个小正方体,2个小正方体涂上颜色的面数之和是2的事件为B则
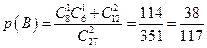 ……………………12分
……………………12分
 ,一面有色的有6个,没有色的有1个。………………3分
,一面有色的有6个,没有色的有1个。………………3分(Ⅰ)
 从这些小正方体中任取1个,含有面数为
从这些小正方体中任取1个,含有面数为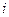 的事件为
的事件为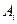 (
(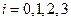 ),则其中至少有两面涂颜色的概率P=
),则其中至少有两面涂颜色的概率P= ;……………………6分
;……………………6分(Ⅱ)根据题意,设从中任取2个小正方体,2个小正方体涂上颜色的面数之和是2的事件为B则
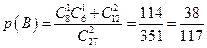 ……………………12分
……………………12分略

练习册系列答案
 开心蛙口算题卡系列答案
开心蛙口算题卡系列答案
相关题目
 分.
分.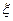 的分布列和数学期望.
的分布列和数学期望.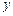
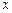
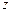
 ,求第三车间中女工比男工少的概率.
,求第三车间中女工比男工少的概率.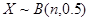 ,且DX=2,则事件“X=1” 的概率为 (用数学作答).
,且DX=2,则事件“X=1” 的概率为 (用数学作答). .设方程
.设方程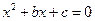 的系数
的系数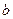 和
和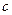 分别是先后抛掷一枚骰子得到的点数.
分别是先后抛掷一枚骰子得到的点数. ,陶艺入选“中国馆·贵宾厅”的概率为
,陶艺入选“中国馆·贵宾厅”的概率为 ”
”

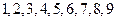 这九个数字中任意取出不同的三个数字.
这九个数字中任意取出不同的三个数字.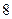 的概率;
的概率;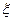 ,求随机变量
,求随机变量