题目内容
2.已知函数f(x)=x2-ax-a.(Ⅰ)若存在实数x,使f(x)<0,求实数a的取值范围;
(Ⅱ)设g(x)=|f(x)|,若任意实数a,存在x0∈[0,1]使不等式g(x0)≥k成立,求实数k的取值范围.
分析 (Ⅰ)配方求出f(x)的最小值由最小值小于0求得实数a的范围;
(Ⅱ)对a分类求出g(x)在区间[0,1]上的最大值为M(a),然后利用单调性求出函数M(a)的最小值求得k的值.
解答 解:(Ⅰ)f(x)=x2-ax-a=$(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4}-a$,
当且仅当$-\frac{{a}^{2}}{4}-a<0$时,存在实数x使f(x)<0,
解得a<-4或a>0;
(Ⅱ)记g(x)=|f(x)|=|$(x-\frac{a}{2})^{2}-\frac{{a}^{2}}{4}-a$|在区间[0,1]上的最大值为M(a),
(1)当$\frac{a}{2}≤0$时,f(x)在区间[0,1]上递增,且f(0)=-a≥0,
∴当x∈[0,1]时,g(x)max=f(x)max=f(1)=1-2a,
(2)当$0<\frac{a}{2}≤1$,即0<a≤2时,f(0)=-a<0,
∴g(x)max=max{$g(\frac{a}{2}),g(1)$}=max{$\frac{{a}^{2}}{4}+a,|1-2a|$}.
①当0$<a≤\frac{1}{2}$时,g(x)max=max{$\frac{{a}^{2}}{4}+a,1-2a$}.
1°当0$<a≤-6+2\sqrt{10}$时,$\frac{{a}^{2}}{4}+a≤1-2a$,∴g(x)max=1-2a;
2°当$-6+2\sqrt{10}<a≤\frac{1}{2}$时,$\frac{{a}^{2}}{4}+a>1-2a$,∴$g(x)_{max}=\frac{{a}^{2}}{4}+a$;
②当$\frac{1}{2}<a≤2$时,g(x)在区间(0,$\frac{a}{2}$)上递增,在($\frac{a}{2},1$)上递减,
∴$g(x)_{max}=g(\frac{a}{2})=\frac{{a}^{2}}{4}+a$;
(3)当$\frac{a}{2}>1$,即a>2时,f(x)在区间[0,1]上递减,且f(0)=-a<0,
∴g(x)max=g(1)=2a-1.
综上所述,$M(a)=\left\{\begin{array}{l}{1-2a,a≤-6+2\sqrt{10}}\\{\frac{{a}^{2}}{4}+a,-6+2\sqrt{10}<a≤2}\\{2a-1,a≥2}\end{array}\right.$,
由题意可知,k≤M(a)min,
当a$≤-6+2\sqrt{10}$时,M(a)为减函数,∴$M(a)_{min}=M(-6+2\sqrt{10})=13-4\sqrt{10}$;
当-6+$2\sqrt{10}<a≤2$时,M(a)为增函数,∴$M(a)_{min}=M(-6+2\sqrt{10})=13-4\sqrt{10}$;
当a≥2时,M(a)=2a-1为增函数,∴M(a)min=M(2)=3.
综上所述,M(a)的最小值为$13-4\sqrt{10}$,即k∈(-∞,13-4$\sqrt{10}$].
点评 本题考查了恒成立问题,着重考查了分类讨论的数学思想方法和数学转化思想方法,正确的分类是解决该题的关键,解决该题需要考生有清晰的思路,属难度较大的题目.

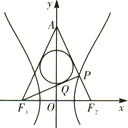 如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( )
如图,已知双曲线$\frac{{x}^{2}}{{a}^{2}}$-$\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)的左、右焦点分别为F1、F2,|F1F2|=8,P是双曲线右支上的一点,直线F2P与y轴交于点A,△APF1的内切圆在边PF1上的切点为Q,若|PQ|=2,则该双曲线的离心率为( )| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
 在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )
在圆柱OO1中,ABCD为轴截面,AB=4,BC=6,D为⊙O1圆周上的点,$\widehat{BP}$的长度等于$\widehat{AP}$长度的2倍,则AD与PC所成角的余弦值为( )| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | -$\frac{\sqrt{3}}{2}$ | D. | $\frac{1}{3}$ |
| A. | $\frac{1}{4}$ab | B. | $\frac{1}{4}$ | C. | $\frac{1}{2}$ab | D. | $\frac{1}{2}$ |