题目内容
求当x≥a时,f(x)的最小值.已知f(x)是定义在{x|x>0}上的增函数,且 .
.(Ⅰ)求f(1)的值;
(Ⅱ)若f(6)=1,解不等式
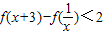 .
.
【答案】分析:(I)取x=y>0,代入已知条件函数的表达式,即可算出f(1)的值为0;
(II)由已知条件证出:当x>0,y>0时,f(xy)=f(x)+f(y),将原不等式转化为f(x(x+3))<2,结合f(6)=1化简整理,可得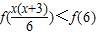 ,最后根据函数的定义域与单调性建立关于x的不等式,解之即可得到不等式的解集.
,最后根据函数的定义域与单调性建立关于x的不等式,解之即可得到不等式的解集.
解答:解:(Ⅰ) 令x=y>0,则f(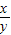 )=f(1)=f(x)-f(x)=0,
)=f(1)=f(x)-f(x)=0,
∴f(1)的值为0;
(Ⅱ) 依题意可得:∵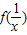 =f(1)-f(x)=-f(x)
=f(1)-f(x)=-f(x)
∴f(xy)=f(y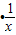 )=f(y)-
)=f(y)-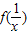 =f(x)+f(y)
=f(x)+f(y)
由此可得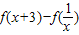 =f(x+3)+f(x)=f[x(x+3)]
=f(x+3)+f(x)=f[x(x+3)]
∴原不等式可化成:f(x(x+3))<2f(6)
故f(x(x+3))-f(6)<f(6),即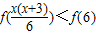
又∵f(x)是定义在{x|x>0}上的增函数,
∴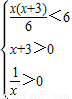 ,解之得:
,解之得: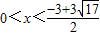
∴不等式的解集为
点评:本题给出满足特殊条件的抽象函数,求函数的值并解关于x的不等式,着重考查了抽象函数的理解和不等式的解法等知识点,属于中档题.
(II)由已知条件证出:当x>0,y>0时,f(xy)=f(x)+f(y),将原不等式转化为f(x(x+3))<2,结合f(6)=1化简整理,可得
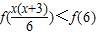 ,最后根据函数的定义域与单调性建立关于x的不等式,解之即可得到不等式的解集.
,最后根据函数的定义域与单调性建立关于x的不等式,解之即可得到不等式的解集.解答:解:(Ⅰ) 令x=y>0,则f(
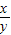 )=f(1)=f(x)-f(x)=0,
)=f(1)=f(x)-f(x)=0,∴f(1)的值为0;
(Ⅱ) 依题意可得:∵
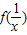 =f(1)-f(x)=-f(x)
=f(1)-f(x)=-f(x)∴f(xy)=f(y
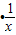 )=f(y)-
)=f(y)-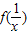 =f(x)+f(y)
=f(x)+f(y)由此可得
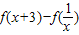 =f(x+3)+f(x)=f[x(x+3)]
=f(x+3)+f(x)=f[x(x+3)]∴原不等式可化成:f(x(x+3))<2f(6)
故f(x(x+3))-f(6)<f(6),即
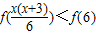
又∵f(x)是定义在{x|x>0}上的增函数,
∴
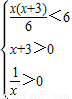 ,解之得:
,解之得: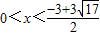
∴不等式的解集为

点评:本题给出满足特殊条件的抽象函数,求函数的值并解关于x的不等式,着重考查了抽象函数的理解和不等式的解法等知识点,属于中档题.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目
