题目内容
已知向量
=(sin(x-
),-1),
=(2,2)且f(x)=
•
+2
①用“五点法”作出函数y=f(x)在长度为一个周期的闭区间的图象.
②求函数f(x)的最小正周期和单调增区间;
③求函数f(x)的最大值,并求出取得最大值时自变量x的取值集合
④函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
⑤当x∈[0,π],求函数y=2sin(x-
)的值域
解:(1)列表
(2)作图
| a |
| π |
| 4 |
| b |
| a |
| b |
①用“五点法”作出函数y=f(x)在长度为一个周期的闭区间的图象.
②求函数f(x)的最小正周期和单调增区间;
③求函数f(x)的最大值,并求出取得最大值时自变量x的取值集合
④函数f(x)的图象可以由函数y=sin2x(x∈R)的图象经过怎样的变换得到?
⑤当x∈[0,π],求函数y=2sin(x-
| π |
| 4 |
解:(1)列表

分析:①利用“五点法”得到五点,列出表格,可画图;
②由周期公式可得周期,根据正弦函数的增区间可得结果;
③根据正弦函数的最大值可求;
④根据图象的平移、伸缩变换规律可得结果;
⑤先由x的范围得x-
的范围,从而可得答案;
②由周期公式可得周期,根据正弦函数的增区间可得结果;
③根据正弦函数的最大值可求;
④根据图象的平移、伸缩变换规律可得结果;
⑤先由x的范围得x-
| π |
| 4 |
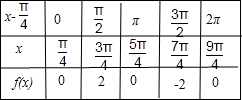
解答:解:①f(x)=2sin(x-
),列表如下:
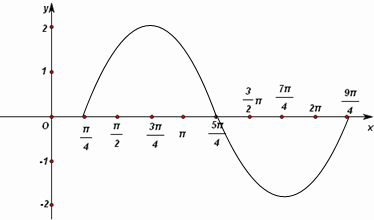
函数f(x)在一个周期内的图象如图所示:
②f(x)的最小正周期为2π,
由2kπ-
≤x-
≤2kπ+
,k∈Z,得2kπ-
≤x≤2kπ+
,k∈Z,
∴f(x)的单调增区间为[2kπ-
,2kπ+
],k∈Z.
③当x-
=2kπ+
,即x=2kπ+
,k∈Z时,f(x)取得最大值为2,
f(x)取得最大值时x的取值集合为:{x|x=2kπ+
,k∈Z}.
④先把y=sin2x的图象上所有点的横坐标伸长为原来的2倍,得到y=sinx的图象,
然后把y=sinx的图象向右平移
个单位,得到y=sin(x-
)的图象,
把y=sin(x-
)图象上所有点的纵坐标伸长为原来的2倍,横坐标不变,得到f(x)=2sin(x-
)的图象;
⑤当x∈[0,π]时,x-
∈[-
,
],
此时函数y=2sin(x-
)的值域为:[-
,2].
| π |
| 4 |

函数f(x)在一个周期内的图象如图所示:

②f(x)的最小正周期为2π,
由2kπ-
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
∴f(x)的单调增区间为[2kπ-
| π |
| 4 |
| 3π |
| 4 |
③当x-
| π |
| 4 |
| π |
| 2 |
| 3π |
| 4 |
f(x)取得最大值时x的取值集合为:{x|x=2kπ+
| 3π |
| 4 |
④先把y=sin2x的图象上所有点的横坐标伸长为原来的2倍,得到y=sinx的图象,
然后把y=sinx的图象向右平移
| π |
| 4 |
| π |
| 4 |
把y=sin(x-
| π |
| 4 |
| π |
| 4 |
⑤当x∈[0,π]时,x-
| π |
| 4 |
| π |
| 4 |
| 3π |
| 4 |
此时函数y=2sin(x-
| π |
| 4 |
| 2 |
点评:本题考查y=Asin(ωx+φ)的图象作法、图象变换及单调性最值,本题综合性较强,但涉及知识较为基础,应熟练掌握.

练习册系列答案
相关题目