Question

已知圆x²+y²=r²在曲线|x|+|y|=4的内部，则半径r的范围是（　　）

• A．0＜r＜2

  2

• B．0＜r＜

  2

• C．0＜r＜2
• D．0＜r＜4

Answer 1

分析：曲线|x|+|y|=4表示边长为4

2

的正方形，x²+y²=r²表示以原点为圆心的圆，要使圆在正方形的内部，即要圆的半径小于等于圆心到正方形边的距离，利用点到直线的距离公式求出此距离，即可得到满足题意的r的范围．

解答：解：根据题意画出图形，如图所示：

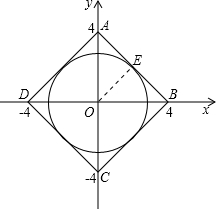
可得曲线|x|+|y|=4表示边长为4

2

的正方形，如图ABCD为正方形，x²+y²=r²表示以原点为圆心的圆，
过O作OE⊥AB，
∵边AB所在直线的方程为x+y=4，
∴|OE|=

4

2

=2

2

，
则满足题意的r的范围是0＜r＜2

2

．
故选A

点评：此题考查了圆的标准方程，以及点到直线的距离公式，利用了数形结合的思想，其中得出曲线|x|+|y|=4表示边长为4

2

的正方形是本题的突破点．