题目内容
若f（x）是R上的奇函数，在[0，+∞）上图象如图所示，则满足xf（x）＜0的解集合是{x|x＜-1，或x＞1}
{x|x＜-1，或x＞1}
．分析：先根据奇函数的对称性画出函数f（x）的图象，再将所解不等式等价转化为不等式组，最后数形结合解不等式即可
解答：解：∵f（x）是R上的奇函数，∴函数图象关于原点对称
∴函数f（x）在R上的图象如图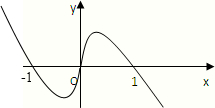
∵xf（x）＜0?
或
?x＞1或x＜-1
∴x•f（x）＜0的解集为{x|x＜-1，或x＞1}
故答案为{x|x＜-1，或x＞1}
∴函数f（x）在R上的图象如图
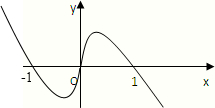
∵xf（x）＜0?
|
|
?x＞1或x＜-1
∴x•f（x）＜0的解集为{x|x＜-1，或x＞1}
故答案为{x|x＜-1，或x＞1}
点评：本题考查了奇函数的图象性质，数形结合解不等式，转化化归的思想方法
练习册系列答案
相关题目