题目内容
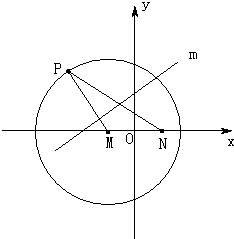 如图,已知N(
如图,已知N(| 5 |
| 5 |
(Ⅰ)求点Q的轨迹C的方程;
(Ⅱ)若直线y=x+b与曲线C相交于A、B两点,求△AOB面积的最大值.
分析:(Ⅰ)利用椭圆的定义,可得点Q在以M、N为焦点的椭圆上,由此可求点Q的轨迹C的方程;
(Ⅱ)直线方程代入椭圆方程,求得|AB|,再求出点O到直线AB的距离,可得△AOB面积,利用基本不等式可求最值.
(Ⅱ)直线方程代入椭圆方程,求得|AB|,再求出点O到直线AB的距离,可得△AOB面积,利用基本不等式可求最值.
解答:解:(Ⅰ)由题意得:|PQ|=|QN|,|QM|+|QP|=|MP|
∴|QM|+|QN|=|MP|
∵P是圆M:(x+
)2+y2=36(M为圆心)上一动点,
∴|MP|=6
∴|QM|+|QN|=6
∵M(-
,0,N(
,0),|MN|=2
<6
∴点Q在以M、N为焦点的椭圆上,即c=
,a=3,
∴b2=a2-c2=4
∴点Q的轨迹方程为
+
=1;
(Ⅱ)直线y=x+b,代入椭圆方程,消去y可得13x2+18bx+9b2-36=0
△=(18b)2-4×13×(9b2-36)>0,∴-
<b<
设A(x1,y1),B(x2,y2),则x1+x2=-
,x1x2=
∴|AB|=
|x1-x2|=
•
设点O到直线AB的距离为d,则d=
∴△AOB面积S=
|AB|d=
•
•
•
=
≤
•
=3
当b=±
时,等号成立
∴当b=±
时,面积的最大值为3.
∴|QM|+|QN|=|MP|
∵P是圆M:(x+
| 5 |
∴|MP|=6
∴|QM|+|QN|=6
∵M(-
| 5 |
| 5 |
| 5 |
∴点Q在以M、N为焦点的椭圆上,即c=
| 5 |
∴b2=a2-c2=4
∴点Q的轨迹方程为
| x2 |
| 9 |
| y2 |
| 4 |
(Ⅱ)直线y=x+b,代入椭圆方程,消去y可得13x2+18bx+9b2-36=0
△=(18b)2-4×13×(9b2-36)>0,∴-
| 13 |
| 13 |
设A(x1,y1),B(x2,y2),则x1+x2=-
| 18b |
| 13 |
| 9b2-36 |
| 13 |
∴|AB|=
| 2 |
12
| ||
| 13 |
| 13-b2 |
设点O到直线AB的距离为d,则d=
| |b| | ||
|
∴△AOB面积S=
| 1 |
| 2 |
| 1 |
| 2 |
12
| ||
| 13 |
| 13-b2 |
| |b| | ||
|
| 6 |
| 13 |
| b2(13-b2) |
| 6 |
| 13 |
| b2+13-b2 |
| 2 |
当b=±
| ||
| 2 |
∴当b=±
| ||
| 2 |
点评:本题考查椭圆的定义与标准方程,考查直线与椭圆的位置关系,考查三角形面积的计算,考查基本不等式,属于中档题.

练习册系列答案
 仁爱英语同步练习册系列答案
仁爱英语同步练习册系列答案 学习实践园地系列答案
学习实践园地系列答案
相关题目
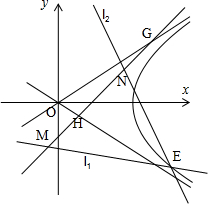
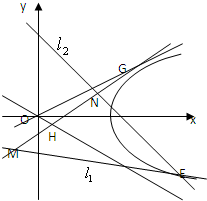
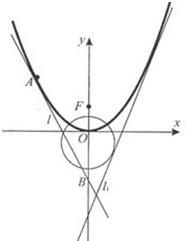 如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点.
如图,已知直线l1:y=2x+m(m<0)与抛物线C1:y=ax2(a>0)和圆C2:x2+(y+1)2=5都相切,F是C1的焦点. (2012•湖北模拟)某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,150),[150,180),[180,210),[210.240),得到频率分布直方图如图,已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人.
(2012•湖北模拟)某校高二年级共有学生1000名,其中走读生750名,住宿生250名,现从该年级采用分层抽样的方法从该年级抽取n名学生进行问卷调查,根据问卷取得了这n名同学每天晚上有效学习时间(单位:分钟)的数据,按照以下区间分为八组:[0,30),[30,60),[60,90),[90,120),[120,150),[150,180),[180,210),[210.240),得到频率分布直方图如图,已知抽取的学生中每天晚上有效学习时间少于60分钟的人数为5人.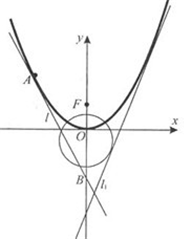 如图,已知直线
如图,已知直线