题目内容
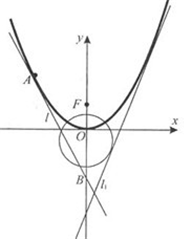 如图,已知直线
如图,已知直线| l | 1 |
(1)求m与a的值;
(2)设A是C1上的一动点,以A为切点作抛物线C1的切线,直线交y轴于点B,以FA,FB为邻边作平行四边形FAMB,证明:点M在一条定直线上;
(3)在(2)的条件下,记点M所在的定直线为l2,直线l2与y轴交点为N,连接MF交抛物线C1于P,Q两点,求△NPQ的面积S的取值范围.
分析:(1)利用圆心到直线的距离等于半径求出m,再利用导函数与切线的关系求出a的值即可;
(2)先求出以A为切点的切线l的方程以及点A,B的表达式,再利用以FA,FB为邻边作平行四边形FAMB,结合向量运算即可求出点M所在的定直线;
(3)设直线MF的方程代入抛物线方程,结合根与系数的关系及三角形面积公式得出面积的表达式,从而可求△NPQ的面积S的取值范围.
(2)先求出以A为切点的切线l的方程以及点A,B的表达式,再利用以FA,FB为邻边作平行四边形FAMB,结合向量运算即可求出点M所在的定直线;
(3)设直线MF的方程代入抛物线方程,结合根与系数的关系及三角形面积公式得出面积的表达式,从而可求△NPQ的面积S的取值范围.
解答:(1)解:由已知,圆C2:x2+(y+1)2=5的圆心为C2(0,-1),半径为
由题设圆心到直线l1:y=2x+m的距离d=
=
,解得m=-6(m=4舍去).
设l1与抛物线的相切点为A0(x0,y0),又y′=2ax,∴2ax0=2
∴x0=
,y0=
,代入直线方程得:
=
-6,∴a=
∴m=-6,a=
;
(2)证明:由(1)知抛物线C1方程为y=
x2,焦点 F(0,
)
设 A(x1,
),由(1)知以A为切点的切线l的方程为y=
x1(x-x1)+
令x=0,得切线l交y轴的B点坐标为(0,-
)
∴
=(x1,
-
),
=(0,-x1,
-
)
∵以FA,FB为邻边作平行四边形FAMB,
∴
=
+
=(x1,-3)
∵F是定点,∴点M在定直线y=-
上;
(3)解:直线MF:y=kx+
,代入y=
x2得
x2-kx-
=0
∴x1+x2=6k,x1x2=-9.
∴S△NPQ=
|NF||x1-x2|=
×3×
=9
∵k≠0,∴S△NPQ>9,
∴NPQ的面积S的取值范围(9,+∞).
| 5 |
由题设圆心到直线l1:y=2x+m的距离d=
| |1+m| | ||
|
| 5 |
设l1与抛物线的相切点为A0(x0,y0),又y′=2ax,∴2ax0=2
∴x0=
| 1 |
| a |
| 1 |
| a |
| 1 |
| a |
| 2 |
| a |
| 1 |
| 6 |
∴m=-6,a=
| 1 |
| 6 |
(2)证明:由(1)知抛物线C1方程为y=
| 1 |
| 6 |
| 3 |
| 2 |
设 A(x1,
| 1 |
| 6 |
| x | 2 1 |
| 1 |
| 3 |
| 1 |
| 6 |
| x | 2 1 |
令x=0,得切线l交y轴的B点坐标为(0,-
| 1 |
| 6 |
| x | 2 1 |
∴
| FA |
| 1 |
| 6 |
| x | 2 1 |
| 3 |
| 2 |
| FB |
| 1 |
| 6 |
| x | 2 1 |
| 3 |
| 2 |
∵以FA,FB为邻边作平行四边形FAMB,
∴
| FM |
| FA |
| FB |
∵F是定点,∴点M在定直线y=-
| 3 |
| 2 |
(3)解:直线MF:y=kx+
| 3 |
| 2 |
| 1 |
| 6 |
| 1 |
| 6 |
| 3 |
| 2 |
∴x1+x2=6k,x1x2=-9.
∴S△NPQ=
| 1 |
| 2 |
| 1 |
| 2 |
| (x1+x2)2-4x1x2 |
| 1+k2 |
∵k≠0,∴S△NPQ>9,
∴NPQ的面积S的取值范围(9,+∞).
点评:本题综合考查圆与椭圆知识,考查直线与椭圆的位置关系,考查向量知识的运用,考查三角形面积的计算,属于中档题.

练习册系列答案
 教学练新同步练习系列答案
教学练新同步练习系列答案 课前课后同步练习系列答案
课前课后同步练习系列答案
相关题目
 如图,已知直线l与抛物线
如图,已知直线l与抛物线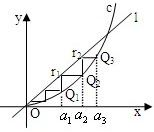 设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
设a>0,如图,已知直线l:y=ax及曲线C:y=x2,C上的点Q1的横坐标为a1(0<a1<a).从C上的点Qn(n≥1)作直线平行于x轴,交直线l于点Pn+1,再从点Pn+1作直线平行于y轴,交曲线C于点Qn+1.Qn(n=1,2,3,…)的横坐标构成数列{an}.
 如图,已知直线L:x=my+1过椭圆C:
如图,已知直线L:x=my+1过椭圆C: 如图,已知直线
如图,已知直线