题目内容
7.已知$\frac{co{s}^{2}α-si{n}^{2}α}{sinα-cosα}$=$\frac{\sqrt{2}}{4}$,则sinαsin($\frac{π}{2}$+α)等于-$\frac{7}{16}$.分析 由条件可得-(sinα+cosα)=$\frac{\sqrt{2}}{4}$,平方并利用诱导公式可得要求式子的值.
解答 解:∵$\frac{co{s}^{2}α-si{n}^{2}α}{sinα-cosα}$=-(sinα+cosα)=$\frac{\sqrt{2}}{4}$,平方可得sinαsin($\frac{π}{2}$+α)=sinαcosα=-$\frac{7}{16}$,
故答案为:-$\frac{7}{16}$.
点评 本题主要考查同角三角函数的基本关系,诱导公式,属于基础题.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
18.函数y=(x+2)ln|x|的图象大致为( )
| A. |  | B. |  | C. | 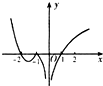 | D. | 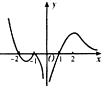 |
12.已知等差数列{an}的前n项和为Sn,若a10=2,S10=10,则a19等于( )
| A. | $\frac{15}{2}$ | B. | 4 | C. | $\frac{19}{4}$ | D. | $\frac{19}{2}$ |
16.已知正项数列{an},a2-1、a3、a7成等比数列,{an}前n项和Sn满足an+12=2Sn+n+4,则(n-6)Sn的最小值为( )
| A. | -26 | B. | -27 | C. | -28 | D. | -30 |
 己知过点M(x1、y1)的直线l1:x1x+3y1y=6与过点N(x2,y2)(其中x2≠x1)的直线l2:x2x+y2y=6的交点E在双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1上,直线MN与两条渐近线分别交与G、H两点,P为GH的中点.
己知过点M(x1、y1)的直线l1:x1x+3y1y=6与过点N(x2,y2)(其中x2≠x1)的直线l2:x2x+y2y=6的交点E在双曲线$\frac{{x}^{2}}{6}$-$\frac{{y}^{2}}{2}$=1上,直线MN与两条渐近线分别交与G、H两点,P为GH的中点.