题目内容

18．函数y=（x+2）ln|x|的图象大致为（　　）
A．B．C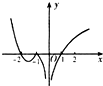．D．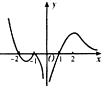

分析 根据函数的零点，单调性及极限思想结合选项使用排除法得出答案．

解答 解：令y=（x+2）ln|x|=0得x=-2或x=1或x=-1，∴该函数由三个零点，排除B；
当x＜-2时，x+2＜0，|x|＞2，∴ln|x|＞ln2＞0，
∴当x＜-2时，y=（x+2）ln|x|＜0，排除C，D．
故选A．

点评 本题考查了函数图象的判断，常从单调性、奇偶性、特殊点、定义域等几个方面进行判断．

练习册系列答案
相关题目
8．“点P（tanα，cosα）在第二象限”是“角α的终边在第四象限”的（　　）
A．充分不必要条件B．必要不充分条件
C．充要条件D．既不充分也不必要条件
9．不等式$\sqrt{\frac{{a}^{2}+{b}^{2}}{2}}$-$\sqrt{ab}$≥λ（$\frac{a+b}{2}$-$\sqrt{ab}$）对任意非负实数a．b恒成立，则正数λ的取值范围为（　　）
A．（0，1]B．（0，$\frac{\sqrt{6}}{2}$]C．（0，$\sqrt{2}$]D．（0，2]
6．已知函数f（x）=$\frac{cx-1}{x+1}$（c为常数），且f（1）=0．
（1）求c的值；
（2）证明函数f（x）在[0，2]上是单调递增函数；
（3）已知函数g（x）=f（ex），判断函数g（x）的奇偶性．
13．已知定义域为R的奇函数满足f（x+4）=f（x），且x∈（0，2）时，f（x）=ln（x2+a），a＞0，若函数f（x）在区间[-4，4]上有9个零点，则实数a的取值范围为（0，1）．
3．幂函数y=f（x）的图象经过点（9，3），则此幂函数的解析式为f（x）=$\sqrt{x}$，x≥0．
10．已知函数f（x）=ax2-2ax+b（a＞0）在区间[-1，4]上有最大值10和最小值1．设g（x）=$\frac{f（x）}{x}$．
（1）求a、b的值；
（2）证明：函数g（x）在[$\sqrt{b}$，+∞）上是增函数；
（3）若不等式g（2x）-k•2x≥0在x∈[-1，1]上有解，求实数k的取值范围．
7．已知$\frac{co{s}^{2}α-si{n}^{2}α}{sinα-cosα}$=$\frac{\sqrt{2}}{4}$，则sinαsin（$\frac{π}{2}$+α）等于-$\frac{7}{16}$．
8．已知函数f（x）=-$\frac{1}{2}$ax2+（1+a）x-lnx（a∈R）．
（Ⅰ）当a＞0时，求函数f（x）的单调递减区间；
（Ⅱ）当a=0时，设函数g（x）=xf（x）．若存在区间[m，n]⊆[$\frac{1}{2}$，+∞），使得函数g（x）在[m，n]上的值域为[k（m+2）-2，k（n+2）-2]，求实数k的取值范围．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网