题目内容
【题目】已知椭圆![]() 的短轴长为
的短轴长为![]() ,离心率为
,离心率为![]() 。
。
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设椭圆![]() 的左,右焦点分别为
的左,右焦点分别为![]() ,
,![]() 左,右顶点分别为
左,右顶点分别为![]() ,
,![]() ,点
,点![]() ,
,![]() ,为椭圆
,为椭圆![]() 上位于
上位于![]() 轴上方的两点,且
轴上方的两点,且![]() ,记直线
,记直线![]() ,
,![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,若
,若![]() ,求直线
,求直线![]() 的方程.
的方程.
【答案】(1)![]() (2)
(2)![]()
【解析】
(1)由题意可得:2b=4![]() ,
,![]() ,a2=b2+c2.联立解出即可得出椭圆C的标准方程.(2)A(﹣3,0),B(3,0),F1(﹣1,0),F2(1,0),设F1M的方程为:x=my﹣1,M(
,a2=b2+c2.联立解出即可得出椭圆C的标准方程.(2)A(﹣3,0),B(3,0),F1(﹣1,0),F2(1,0),设F1M的方程为:x=my﹣1,M(![]() ),(
),(![]() >0),直线F1M与椭圆的另一个交点为M′(
>0),直线F1M与椭圆的另一个交点为M′(![]() ).由
).由![]() 根据对称性可得:
根据对称性可得:![]() .直线方程与椭圆方程联立化为:(8m2+9)y2﹣16my﹣64=0,根据根与系数的关系及其
.直线方程与椭圆方程联立化为:(8m2+9)y2﹣16my﹣64=0,根据根与系数的关系及其![]() ,得
,得![]() 0,联立解得m.
0,联立解得m.
(1)由题意,得![]() ,
,![]() .
.
又![]() ,∴
,∴![]() ,
,![]() ,
,![]() .
.
∴椭圆C的标准方程为![]()
(2)由(1),可知![]() ,
,![]() ,
,![]() .
.
据题意,直线![]() 的方程为
的方程为![]()
记直线![]() 与椭圆的另一交点为
与椭圆的另一交点为![]() ,设
,设![]() ,
,![]() .
.
∵![]() ,根据对称性,得
,根据对称性,得![]() .
.
联立![]() ,
,
消去![]() ,得
,得![]() ,其判别式
,其判别式![]() ,
,
∴![]() ,
,![]() .①
.①
由![]() ,得
,得![]() ,即
,即![]() .②
.②
由①②,解得![]() ,
,![]()
∵![]() ,∴
,∴![]() .
.
∴![]() .∴
.∴![]() .
.
∴直线![]() 的方程为
的方程为![]() ,即
,即![]() .
.

 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案【题目】已知抛物线C:y2=2px(p>0)与圆![]() 无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
无公共点,过抛物线C上一点M作圆D的两条切线,切点分别为E,F,当点M在抛物线C上运动时,直线EF都不通过的点构成一个区域,求这个区域的面积的取值范围.
【题目】为了让税收政策更好的为社会发展服务,国家在修订《中华人民共和国个人所得税法》之后,发布了《个人所得税专项附加扣除暂行办法》,明确“专项附加扣除”就是子女教育、继续教育大病医疗、住房贷款利息、住房租金赠养老人等费用,并公布了相应的定额扣除标准,决定自2019年1月1日起施行,某机关为了调查内部职员对新个税方案的满意程度与年龄的关系,通过问卷调查,整理数据得如下2×2列联表:
40岁及以下 | 40岁以上 | 合计 | |
基本满意 | 15 | 30 | 45 |
很满意 | 25 | 10 | 35 |
合计 | 40 | 40 | 80 |
(1)根据列联表,能否有99%的把握认为满意程度与年龄有关?
(2)为了帮助年龄在40岁以下的未购房的8名员工解决实际困难,该企业拟员工贡献积分![]() (单位:分)给予相应的住房补贴
(单位:分)给予相应的住房补贴![]() (单位:元),现有两种补贴方案,方案甲:
(单位:元),现有两种补贴方案,方案甲:![]() ;方案乙:
;方案乙: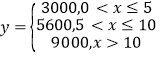 .已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“
.已知这8名员工的贡献积分为2分,3分,6分,7分,7分,11分,12分,12分,将采用方案甲比采用方案乙获得更多补贴的员工记为“![]() 类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“
类员工”.为了解员工对补贴方案的认可度,现从这8名员工中随机抽取4名进行面谈,求恰好抽到3名“![]() 类员工”的概率。
类员工”的概率。
附:![]() ,其中
,其中![]() .
.
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |
【题目】为研究男、女生的身高差异,现随机从高二某班选出男生、女生各10人,并测量他们的身高,测量结果如下(单位:厘米):
男:164 178 174 185 170 158 163 165 161 170
女:165 168 156 170 163 162 158 153 169 172
(1)根据测量结果完成身高的茎叶图(单位:厘米),并分别求出男、女生身高的平均值.
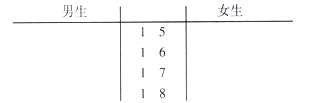
(2)请根据测量结果得到20名学生身高的中位数![]() (单位:厘米),将男、女生身高不低于
(单位:厘米),将男、女生身高不低于![]() 和低于
和低于![]() 的人数填入下表中,并判断是否有
的人数填入下表中,并判断是否有![]() 的把握认为男、女生身高有差异?
的把握认为男、女生身高有差异?
人数 | 男生 | 女生 |
身高 | ||
身高 |
参照公式:![]()
| 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(3)若男生身高低于165厘米为偏矮,不低于165厘米且低于175厘米为正常,不低于175厘米为偏高.假设可以用测量结果的频率代替概率,试求从高二的男生中任意选出2人,恰有1人身高属于正常的概率.