题目内容
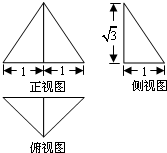一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体（ ）分析：确定直观图的形状，计算外接球的半径，即可得到结论．
解答：
解：由三视图可知，这是侧面ACD⊥ABC，高DE=
的三棱锥，AC=2，EB=1，
所以三棱锥的体积为
×
×2×
=
，
设外接球的圆心为0，半径为x，则OE=
-x，
在直角三角形OEC中，OE2+CE2=OC2，即（
-x）2+1=x2，解得半径x=
，
所以外接球的表面积为4πx2=4π×(
)2=
，
所以A，B，C都不正确，
故选D．
解：由三视图可知，这是侧面ACD⊥ABC，高DE=| 3 |
所以三棱锥的体积为
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| ||
| 3 |
设外接球的圆心为0，半径为x，则OE=
| 3 |
在直角三角形OEC中，OE2+CE2=OC2，即（
| 3 |
2
| ||
| 3 |
所以外接球的表面积为4πx2=4π×(
2
| ||
| 3 |
| 16π |
| 3 |
所以A，B，C都不正确，
故选D．
点评：本题考查三视图，考查直观图，确定直观图的形状，计算外接球的半径是关键
练习册系列答案
津桥教育计算小状元系列答案
相关题目
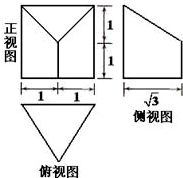
（2013•房山区二模）一个几何体的三视图如图所示，则这个几何体的表面积为（ ）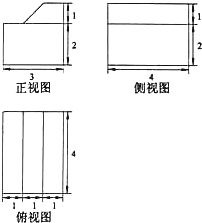
（2012•天津）一个几何体的三视图如图所示（单位：m），则该几何体的体积为
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的表面积为
（2010•河东区一模）一个几何体的三视图如图所示，则该几何体（不考虑接触点）的表面积为