题目内容
定义区间 的长度均为
的长度均为 ,其中
,其中 。已知实数
。已知实数 ,则满足
,则满足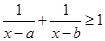 的
的 构成的区间的长度之和为 .
构成的区间的长度之和为 .
2
解析试题分析:原不等式等价于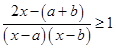 。当
。当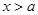 或
或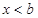 时,原不等式等价于
时,原不等式等价于 。设
。设 ,则
,则 。设
。设 的两个根分别为
的两个根分别为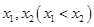 ,则满足
,则满足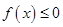 的
的 构成的区间为
构成的区间为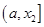 ,区间的长度为
,区间的长度为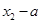 。当
。当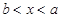 时,同理可得满足
时,同理可得满足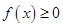 的
的 构成的区间为
构成的区间为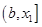 ,区间的长度为
,区间的长度为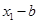 。由韦达定理,
。由韦达定理,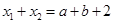 ,所以满足条件的
,所以满足条件的 构成的区间的长度之和为
构成的区间的长度之和为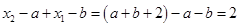
考点:本题考查了一元二次方程的根
点评:此类问题通常转化为一元二次方程根的问题,难度比较大,关键是掌握一元二次方程中的韦达定理及根的分布

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
 等于 .
等于 . ,在
,在 上是减少的,则
上是减少的,则 的取值范围是
的取值范围是  中,若
中,若 ,则
,则 的值是
的值是  的所有切线中,斜率最小的切线方程是 。
的所有切线中,斜率最小的切线方程是 。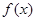 的定义域为D,若对任意的
的定义域为D,若对任意的 、
、 ,当
,当 时,都有
时,都有 ,则称函数
,则称函数 在
在 上为“非减函数”,且满足以下三个条件:(1)
上为“非减函数”,且满足以下三个条件:(1) ;(2)
;(2) ;(3)
;(3) ,则
,则 、
、 .
. ,若
,若 则
则 ________;
________; 的值域是 .
的值域是 . 的定义域是
的定义域是