题目内容
(15分)已知定义在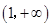 上的函数
上的函数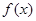 =
=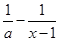
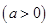
(Ⅰ)若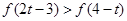 ,求实数
,求实数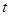 的取值范围;
的取值范围;
(Ⅱ)若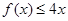 对
对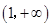 上的任意
上的任意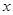 都成立,求实数
都成立,求实数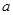 的取值范围;
的取值范围;
(Ⅲ)若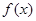 在[m,n]上的值域是[m,n](m≠n),求实数
在[m,n]上的值域是[m,n](m≠n),求实数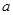 的取值范围
的取值范围
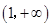 上的函数
上的函数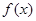 =
=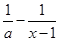
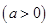
(Ⅰ)若
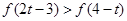 ,求实数
,求实数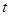 的取值范围;
的取值范围;(Ⅱ)若
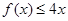 对
对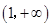 上的任意
上的任意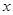 都成立,求实数
都成立,求实数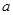 的取值范围;
的取值范围;(Ⅲ)若
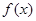 在[m,n]上的值域是[m,n](m≠n),求实数
在[m,n]上的值域是[m,n](m≠n),求实数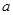 的取值范围
的取值范围 解:(1)
 ;(2)
;(2)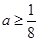 ;(3)
;(3)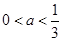

第一问中利用单调性可知,由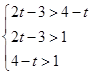 解得
解得
第二问中,由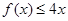 得
得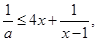
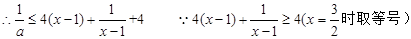
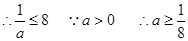
(3)中由于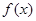 在
在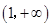 单调递增
单调递增
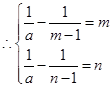
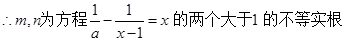
令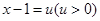
由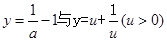 的图像可得
的图像可得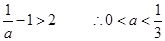

本题也可以转化为根的分布求解,同样给分.
解:(1)由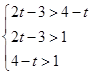 解得
解得
(2)由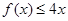 得
得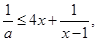
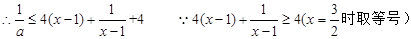
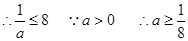
(3)由于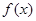 在
在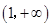 单调递增
单调递增
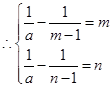
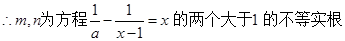
令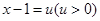
由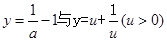 的图像可得
的图像可得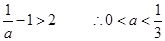

本题也可以转化为根的分布求解,同样给分.
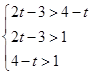 解得
解得
第二问中,由
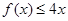 得
得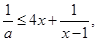
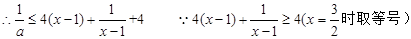
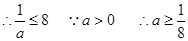
(3)中由于
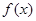 在
在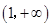 单调递增
单调递增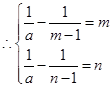
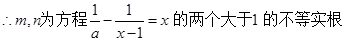
令
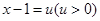
由
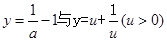 的图像可得
的图像可得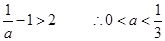

本题也可以转化为根的分布求解,同样给分.
解:(1)由
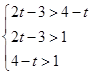 解得
解得
(2)由
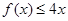 得
得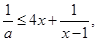
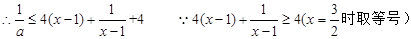
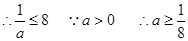
(3)由于
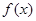 在
在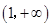 单调递增
单调递增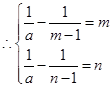
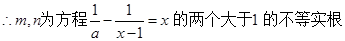
令
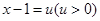
由
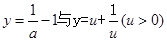 的图像可得
的图像可得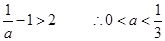

本题也可以转化为根的分布求解,同样给分.

练习册系列答案
相关题目
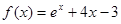 的零点所在的区间为
的零点所在的区间为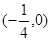
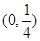
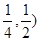
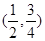
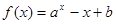 的零点
的零点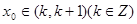 ,其中常数a,b满足
,其中常数a,b满足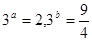 ,则
,则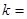
 ,且函数
,且函数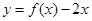 恰有3个不同的零点,则实数a 的取值范围是( )
恰有3个不同的零点,则实数a 的取值范围是( )
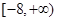
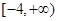

 的一个正数零点附近的函数值用二分法计算,参考数据如下:
的一个正数零点附近的函数值用二分法计算,参考数据如下:





 的一个近似根(精确度为0.1)为___▲___.
的一个近似根(精确度为0.1)为___▲___. 满足
满足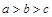 ,且
,且 .若
.若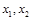 为方程
为方程 的两个实数根,则
的两个实数根,则 的取值范围为【 】.
的取值范围为【 】.
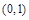


 )x有两个零点x1,x2,则有
)x有两个零点x1,x2,则有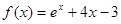 的零点所在的区间为( )
的零点所在的区间为( )



 有一个零点
有一个零点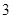 ,那么函数
,那么函数 的零点是
的零点是


