题目内容
已知 ,且函数
,且函数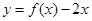 恰有3个不同的零点,则实数a 的取值范围是( )
恰有3个不同的零点,则实数a 的取值范围是( )
 ,且函数
,且函数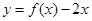 恰有3个不同的零点,则实数a 的取值范围是( )
恰有3个不同的零点,则实数a 的取值范围是( )A. | B.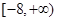 | C.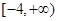 | D. |
C
解:因为当x≥0的时候,f(x)=f(x-2),所以所有大于等于0的x代入得到的f(x)相当于在[-2,0)重复的周期函数
x∈[-2,0)时,y=a-x2-4x=4+a-(x+2)2,对称轴x=-2,顶点(-2,4+a)
(1)如果a<-4,函数y=f(x)-2x至多有2个不同的零点;
(2)如果a=-4,则y有一个零点在区间(-2,0),有一个零点在(-∞,-2),一个零点是原点;
(3)如果a>-4,则有一个零点在(-∞,-2),y右边有两个零点,
故实数a的取值范围是[-4,+∞)
x∈[-2,0)时,y=a-x2-4x=4+a-(x+2)2,对称轴x=-2,顶点(-2,4+a)
(1)如果a<-4,函数y=f(x)-2x至多有2个不同的零点;
(2)如果a=-4,则y有一个零点在区间(-2,0),有一个零点在(-∞,-2),一个零点是原点;
(3)如果a>-4,则有一个零点在(-∞,-2),y右边有两个零点,
故实数a的取值范围是[-4,+∞)

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 的两零点间的距离为1,则
的两零点间的距离为1,则 的值为( )
的值为( )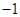 或1
或1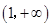 上的函数
上的函数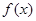 =
=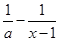
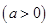
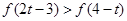 ,求实数
,求实数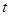 的取值范围;
的取值范围;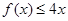 对
对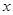 都成立,求实数
都成立,求实数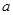 的取值范围;
的取值范围; 有一个正根和一个负根,则实数
有一个正根和一个负根,则实数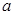 的取值范围是__________________.
的取值范围是__________________. ,其中m是实数
,其中m是实数 有零点,求m的取值范围;(7分)
有零点,求m的取值范围;(7分) 的解集为A,若
的解集为A,若 ,求m的取值范围。(7分)
,求m的取值范围。(7分) ,
,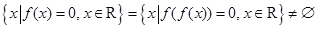 ,则满足条件的所有实数a的取值范围为 ( )
,则满足条件的所有实数a的取值范围为 ( ) <4
<4
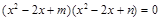 的四个实根组成一个首项为
的四个实根组成一个首项为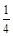 的等差数列,则
的等差数列,则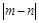 等于( )
等于( )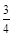
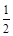
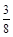
 .
.