Question

【题目】已知函数f（x）=|x﹣1|+|x﹣a|．
（1）若a≤2，解不等式f（x）≥2；
（2）若a＞1，x∈R，f（x）+|x﹣1|≥1，求实数a的取值范围．

Answer 1

【答案】
（1）解：当f（x）=|x﹣1|+|x﹣2|= 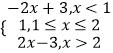，而f（x）≥2，

解得 或

（2）解：令F（x）=f（x）+|x﹣1|，则F（x）= ，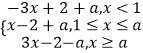

所以当x=1时，F（x）有最小值F（1）=a﹣1，

只需a﹣1≥1，解得a≥2，

所以实数a的取值范围是[2，+∞）

【解析】（1）通过讨论x的范围，求出各个区间的解集，取并集即可；（2）令F（x）=f（x）+|x﹣1|，求出F（x）的最小值，从而求出a的范围即可．
【考点精析】掌握绝对值不等式的解法是解答本题的根本，需要知道含绝对值不等式的解法：定义法、平方法、同解变形法，其同解定理有；规律：关键是去掉绝对值的符号．