题目内容
15.已知以C为圆心的动圆过定点A(-3,0),且与圆B:(x-3)2+y2=64(B为圆心)相切,点C的轨迹为曲线T.设Q为曲线T上(不在x轴上)的动点,过点A作OQ(O为坐标原点)的平行线交曲线T于M,N两点.(I)求曲线T的方程;
(Ⅱ)是否存在常数λ,使$\overrightarrow{AM}•\overrightarrow{AN}=λ{\overrightarrow{OQ}^2}$总成立?若存在,求λ;若不存在,说明理由.
分析 (Ⅰ)判断两圆相内切,求出|CA|+|CB|=8,说明C点的轨迹是以A,B为焦点的椭圆,求出长轴长,短轴长,即可得到曲线T的方程.
(Ⅱ)当直线MN斜率不存在时,求出MN的方程为:x=0,然后求出λ;当直线MN斜率存在时,设M(x1,y1),N(x2,y2),MN:y=k(x+3),则OQ:y=kx,联立$\left\{{\begin{array}{l}{7{x^2}+16{y^2}=112}\\{y=k(x+3)}\end{array}}\right.$,利用韦达定理,推出$\overrightarrow{AM}•\overrightarrow{AN}$的表达式,通过$\left\{\begin{array}{l}7{x}^{2}+16{y}^{2}=112\\ y=kx\end{array}\right.$求出${\overrightarrow{OQ}}^{2}$,利用$\overrightarrow{AM}•\overrightarrow{AN}=λ{\overrightarrow{OQ}}^{2}$可解得λ.
解答 解:(Ⅰ)∵A(-3,0)在圆B的内部,∴两圆相内切,所以|CA|+|CB|=8>6,
∴C点的轨迹是以A,B为焦点的椭圆,2a=8,a=4;2c=6,∴c=3,b=$\sqrt{{4}^{2}-{3}^{2}}$=$\sqrt{7}$
∴曲线T的方程为:$\frac{{x}^{2}}{16}+\frac{{y}^{2}}{7}=1$.…(4分)
(Ⅱ)当直线MN斜率不存在时,MN的方程为:x=0,∴${\overrightarrow{OQ}}^{2}=7$.
∴$\overrightarrow{AM}•\overrightarrow{AN}=|\overrightarrow{AM}|•|\overrightarrow{AN}|•cosπ=7λ$,则$λ=-\frac{7}{16}$;…(5分)
当直线MN斜率存在时,设M(x1,y1),N(x2,y2),MN:y=k(x+3),则OQ:y=kx,
由$\left\{{\begin{array}{l}{7{x^2}+16{y^2}=112}\\{y=k(x+3)}\end{array}}\right.$得(7+16k2)x2+96k2x+144k2-112=0,
则${x}_{1}+{x}_{2}=\frac{-96{k}^{2}}{7+16{k}^{2}}$,${x_1}•{x_2}=\frac{{144{k^2}-112}}{{7+16{k^2}}}$,…(8分)
∴y1y2=k2[(x1+3)(x2+3)]=k2[x1x2+3(x1+x2)+9]=$\frac{-49{k}^{2}}{7+16{k}^{2}}$.
$\overrightarrow{AM}•\overrightarrow{AN}$=y1y2+[(x1+3)(x2+3)]═$\frac{-49{(k}^{2}+1)}{7+16{k}^{2}}$…(10分)
由$\left\{{\begin{array}{l}{7{x^2}+16{y^2}=112}\\{y=kx}\end{array}}\right.$得7x2+16k2x2=112,则x2=$\frac{112}{7+16{k}^{2}}$,
∴${\overrightarrow{OQ}}^{2}={x}^{2}+{y}^{2}=(1+{k}^{2}){x}^{2}=\frac{112(1+{k}^{2})}{7+16{k}^{2}}$,由$\overrightarrow{AM}•\overrightarrow{AN}=λ{\overrightarrow{OQ}}^{2}$可解得$λ=-\frac{7}{16}$.
综上,存在常数$λ=-\frac{7}{16}$,使$\overrightarrow{AM}•\overrightarrow{AN}=λ{\overrightarrow{OQ}}^{2}$总成立.…(13分)
点评 本题考查直线与椭圆的综合应用,椭圆的轨迹方程的求法,向量与椭圆的综合应用,考查分析问题解决问题的能力.

 春雨教育同步作文系列答案
春雨教育同步作文系列答案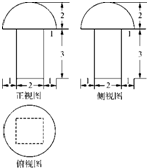
| A. | 12+$\frac{4π}{3}$ | B. | 12+$\frac{16π}{3}$ | C. | 4+$\frac{16π}{3}$ | D. | 4+$\frac{4π}{3}$ |
| A. | 0.977 | B. | 0.954 | C. | 0.628 | D. | 0.477 |
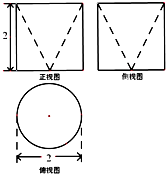
| A. | $\frac{4}{3}$π | B. | 7π | C. | (5+$\sqrt{5}$)π | D. | (4+$\sqrt{5}$)π |