题目内容
【题目】已知直线y=k(x+ ![]() )与曲线y=
)与曲线y= ![]() 恰有两个不同交点,记k的所有可能取值构成集合A;P(x,y)是椭圆
恰有两个不同交点,记k的所有可能取值构成集合A;P(x,y)是椭圆 ![]() 上一动点,点P1(x1 , y1)与点P关于直线y=x+l对称,记
上一动点,点P1(x1 , y1)与点P关于直线y=x+l对称,记 ![]() 的所有可能取值构成集合B,若随机地从集合A,B中分别抽出一个元素λ1 , λ2 , 则λ1>λ2的概率是 .
的所有可能取值构成集合B,若随机地从集合A,B中分别抽出一个元素λ1 , λ2 , 则λ1>λ2的概率是 .
【答案】![]()
【解析】解:∵y= ![]() , ∴x=y2 , 代入y=k(x+
, ∴x=y2 , 代入y=k(x+ ![]() )得y=k(y2+
)得y=k(y2+ ![]() ),
),
整理得ky2﹣y+ ![]() =0,
=0,
直线y=k(x+ ![]() )与曲线y=
)与曲线y= ![]() 恰有两个不同交点,
恰有两个不同交点,
等价为ky2﹣y+ ![]() =0有两个不同的非负根,
=0有两个不同的非负根,
即△=1﹣k2>0,且 ![]() >0,
>0,
解得0<k<1,
∴A={k|0<k<1}.
P1(x1 , y1)关于直线y=x+1的对称点为P(y1﹣1,x1+1),
P是椭圆 ![]() 上一动点,
上一动点,
∴﹣4≤y1﹣1≤4,
即﹣1≤ ![]() ≤1,
≤1,
设b= ![]() ,则﹣1≤b≤1,
,则﹣1≤b≤1,
∴B={b|﹣1≤b≤1}.
∴随机的从集合A,B中分别抽取一个元素λ1 , λ2 ,
则λ1>λ2等价为 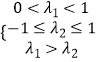 ,
,
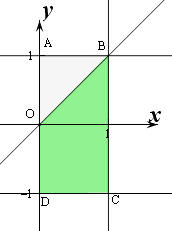
则对应的图象如图:
则λ1>λ2的概率是 ![]() ,
,
所以答案是: ![]() .
.
【考点精析】掌握几何概型是解答本题的根本,需要知道几何概型的特点:1)试验中所有可能出现的结果(基本事件)有无限多个;2)每个基本事件出现的可能性相等.

练习册系列答案
相关题目