题目内容
(12分)设函数f(x)＝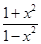
.
(1)求f(x)的定义域；(2)判断f(x)的奇偶性；(3)求证：f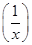
＋f(x)＝0.
【答案】
） (1)函数f(x)的定义域为{x∈R|x≠±1}．(2) f(x)为偶函数．(3)证明：见解析。
【解析】本试题主要是考查了函数的定义域和奇偶性的判定以及函数解析式的运用
（1）因为由解析式知，函数应满足1－x2≠0，即x≠±1.
∴函数f(x)的定义域为{x∈R|x≠±1}．
（2）由(1)知定义域关于原点对称，
f(－x)＝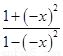
＝
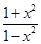＝f(x)
（（3）根据解析式求解f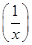
＋f(x)＝0.即可得证。
解：(1)由解析式知，函数应满足1－x2≠0，即x≠±1.
∴函数f(x)的定义域为{x∈R|x≠±1}．
(2)由(1)知定义域关于原点对称，
f(－x)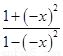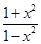＝＝＝f(x)．
∴f(x)为偶函数．
(3)证明：∵f＝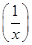
＝
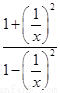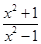，f(x)＝，
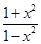∴f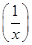＋f(x)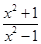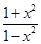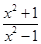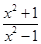＝＋＝－＝0.
练习册系列答案
相关题目
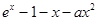
，函数f(x)的图像与x轴的交点也在函数g(x)的图像上，且在此点处f(x)与g(x)有公切线.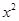
－mx－1.