Question

（本小题满分12分）设函数f(x)＝m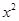－mx－1.

（1）若对于一切实数x，f(x)<0恒成立，求m的取值范围；

（2）对于x∈[1,3]，f(x)<0恒成立，求m的取值范围．

 

Answer 1

【答案】

 

（1）－4<m≤0

（2）m<

【解析】

解：(1)要使mx2－mx－1<0恒成立，

若m＝0，显然－1<0；

若m≠0，则⇒－4<m<0.

∴－4<m≤0.

(2)当m＝0时，f(x)＝－1<0显然恒成立；

当m>0时，由于f(1)＝－1<0，要使f(x)<0在x∈[1,3]上恒成立，只要f(3)<0即可．

即9m－3m－1<0得m<，即0<m<；

当m<0时，若Δ<0，由(1)知显然成立，此时－4<m<0；若Δ≥0，则m≤－4，由于函数f(x)<0在x∈[1,3]上恒成立，只要f(1)<0即可，此时f(1)＝－1<0显然成立，综上可知：m<.