题目内容
已知函数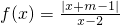 ,m>0且f(1)=-1.
,m>0且f(1)=-1.
(1)求实数m的值;
(2)判断函数y=f(x)在区间(-∞,m-1]上的单调性,并用函数单调性的定义证明;
(3)求实数k的取值范围,使得关于x的方程f(x)=kx分别为:
①有且仅有一个实数解;
②有两个不同的实数解;
③有三个不同的实数解.
解:(1)由f(1)=-1,得 ,|m|=1,
,|m|=1,
∵m>0,∴m=1. (4分)
(2)由(1),m=1,从而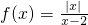 ,只需研究f(x)在(-∞,0]上的单调性.
,只需研究f(x)在(-∞,0]上的单调性.
当x∈(-∞,0]时, .
.
设x1,x2∈(-∞,0],且x1<x2,则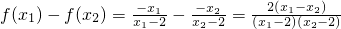 ,(6分)
,(6分)
∵x1<x2≤0,∴x1-x2<0,x1-2<0,x2-2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)在区间(-∞,0]上是单调递增函数. (10分)
(3)原方程即为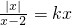 …①
…①
x=0恒为方程①的一个解. (11分)
若x<0时方程①有解,则 ,解得
,解得 ,
,
由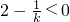 ,得
,得 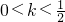 ; (13分)
; (13分)
若x>0且x≠2时方程①有解,则 ,解得
,解得 ,
,
由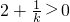 且
且 ,得
,得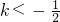 或k>0. (15分)
或k>0. (15分)
综上可得,当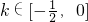 时,方程f(x)=kx有且仅有一个解;
时,方程f(x)=kx有且仅有一个解;
当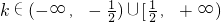 时,方程f(x)=kx有两个不同解;
时,方程f(x)=kx有两个不同解;
当 时,方程f(x)=kx有三个不同解. (18分)
时,方程f(x)=kx有三个不同解. (18分)
分析:(1)将已知条件f(1)=-1,解得|m|=1,再结合m是正数,可得m=1;
(2)将(1)的结论代入得(-∞,m-1]=(-∞,0]根据函数单调性的定义,可设x1,x2∈(-∞,0],且x1<x2,通过作差化简整理,最后得到f(x1)-f(x2)<0,说明函数在区间(-∞,m-1]上是个增函数;
(3)首先,方程f(x)=kx有一个解x=0,然后分x>0和x<0加以讨论:当x>0且x≠2时,方程转化为 ,得到
,得到 ,解不等式得
,解不等式得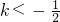 或k>0;当x<0时,则
或k>0;当x<0时,则 ,解得
,解得 ,解不等式得
,解不等式得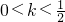 .最后综合可得方程f(x)=kx解集的情况.
.最后综合可得方程f(x)=kx解集的情况.
点评:本题以含有绝对值的分式函数的形式为例,考查了函数零点的分布与单调性等知识点,属于难题.
 ,|m|=1,
,|m|=1,∵m>0,∴m=1. (4分)
(2)由(1),m=1,从而
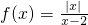 ,只需研究f(x)在(-∞,0]上的单调性.
,只需研究f(x)在(-∞,0]上的单调性.当x∈(-∞,0]时,
 .
.设x1,x2∈(-∞,0],且x1<x2,则
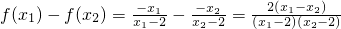 ,(6分)
,(6分)∵x1<x2≤0,∴x1-x2<0,x1-2<0,x2-2<0,
∴f(x1)-f(x2)<0,即f(x1)<f(x2).
∴函数f(x)在区间(-∞,0]上是单调递增函数. (10分)
(3)原方程即为
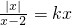 …①
…①x=0恒为方程①的一个解. (11分)
若x<0时方程①有解,则
 ,解得
,解得 ,
,由
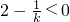 ,得
,得 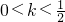 ; (13分)
; (13分)若x>0且x≠2时方程①有解,则
 ,解得
,解得 ,
,由
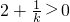 且
且 ,得
,得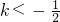 或k>0. (15分)
或k>0. (15分)综上可得,当
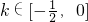 时,方程f(x)=kx有且仅有一个解;
时,方程f(x)=kx有且仅有一个解;当
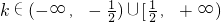 时,方程f(x)=kx有两个不同解;
时,方程f(x)=kx有两个不同解;当
 时,方程f(x)=kx有三个不同解. (18分)
时,方程f(x)=kx有三个不同解. (18分)分析:(1)将已知条件f(1)=-1,解得|m|=1,再结合m是正数,可得m=1;
(2)将(1)的结论代入得(-∞,m-1]=(-∞,0]根据函数单调性的定义,可设x1,x2∈(-∞,0],且x1<x2,通过作差化简整理,最后得到f(x1)-f(x2)<0,说明函数在区间(-∞,m-1]上是个增函数;
(3)首先,方程f(x)=kx有一个解x=0,然后分x>0和x<0加以讨论:当x>0且x≠2时,方程转化为
 ,得到
,得到 ,解不等式得
,解不等式得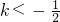 或k>0;当x<0时,则
或k>0;当x<0时,则 ,解得
,解得 ,解不等式得
,解不等式得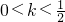 .最后综合可得方程f(x)=kx解集的情况.
.最后综合可得方程f(x)=kx解集的情况.点评:本题以含有绝对值的分式函数的形式为例,考查了函数零点的分布与单调性等知识点,属于难题.

练习册系列答案
 天天向上口算本系列答案
天天向上口算本系列答案
相关题目
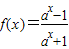 (a>0且a≠1)
(a>0且a≠1)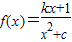 (c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c.
(c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c. (c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c
(c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c 恒成立,求k的取值范围.
恒成立,求k的取值范围.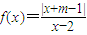 ,m>0且f(1)=-1.
,m>0且f(1)=-1.