题目内容
已知函数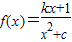 (c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c.
(c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c.(Ⅰ)求函数f(x)的另一个极值点;
(Ⅱ)求函数f(x)的极大值M和极小值m,并求M-m≥1时k的取值范围.
【答案】分析:(Ⅰ)原函数恰有一个极大值点和一个极小值点就是导函数恰有两个不等实根,利用根与系数的关系求出另一根即可.
(Ⅱ)根据开口向上和向下两种情况分别找到M-m,再解M-m≥1即可.
解答:解:(Ⅰ)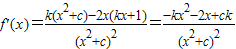 ,
,
由题意知f'(-c)=0,即得c2k-2c-ck=0,(*)
∵c≠0,∴k≠0.
由f'(x)=0得-kx2-2x+ck=0,
由韦达定理知另一个极值点为x=1(或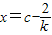 ).
).
(Ⅱ)由(*)式得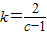 ,即
,即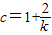 .
.
当c>1时,k>0;当0<c<1时,k<-2.
(i)当k>0时,f(x)在(-∞,-c)和(1,+∞)内是减函数,在(-c,1)内是增函数.
∴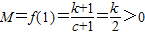 ,
,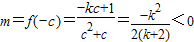 ,
,
由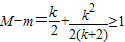 及k>0,解得
及k>0,解得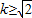 .
.
(ii)当k<-2时,f(x)在(-∞,-c)和(1,+∞)内是增函数,在(-c,1)内是减函数.
∴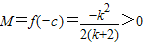 ,
,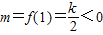
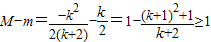 恒成立.
恒成立.
综上可知,所求k的取值范围为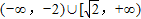 .
.
点评:本题考查利用导函数来研究函数的极值以及对分类讨论思想的考查.分类讨论思想在数学中是非常重要的思想之一,所以希望能加强这方面的训练.
(Ⅱ)根据开口向上和向下两种情况分别找到M-m,再解M-m≥1即可.
解答:解:(Ⅰ)
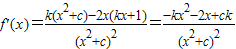 ,
,由题意知f'(-c)=0,即得c2k-2c-ck=0,(*)
∵c≠0,∴k≠0.
由f'(x)=0得-kx2-2x+ck=0,
由韦达定理知另一个极值点为x=1(或
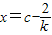 ).
).(Ⅱ)由(*)式得
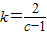 ,即
,即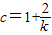 .
.当c>1时,k>0;当0<c<1时,k<-2.
(i)当k>0时,f(x)在(-∞,-c)和(1,+∞)内是减函数,在(-c,1)内是增函数.
∴
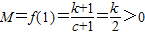 ,
,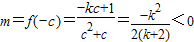 ,
,由
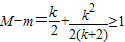 及k>0,解得
及k>0,解得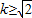 .
.(ii)当k<-2时,f(x)在(-∞,-c)和(1,+∞)内是增函数,在(-c,1)内是减函数.
∴
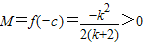 ,
,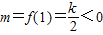
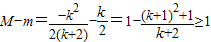 恒成立.
恒成立.综上可知,所求k的取值范围为
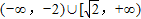 .
.点评:本题考查利用导函数来研究函数的极值以及对分类讨论思想的考查.分类讨论思想在数学中是非常重要的思想之一,所以希望能加强这方面的训练.

练习册系列答案
相关题目
 (c>0且c≠1,
(c>0且c≠1, k>0)恰有一个极大值点和一个极小值点,其中一个是
k>0)恰有一个极大值点和一个极小值点,其中一个是 .则函数
.则函数 的极大值为 。(用只含k的代数式表示)
的极大值为 。(用只含k的代数式表示)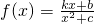 (c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c
(c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c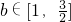 恒成立,求k的取值范围.
恒成立,求k的取值范围.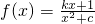 (c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c.
(c>0且c≠1,k∈R)恰有一个极大值点和一个极小值点,其中一个是x=-c. (c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c
(c>0且c≠1,k>0)恰有一个极大值点和一个极小值点,且其中一个极值点是x=-c 恒成立,求k的取值范围.
恒成立,求k的取值范围.