题目内容
已知函数f(x)＝－x2＋2ex＋m－1，g(x)＝x＋
(x>0)．
(1)若g(x)＝m有零点，求m的取值范围；
(2)确定m的取值范围，使得g(x)－f(x)＝0有两个相异实根．
(x>0)．(1)若g(x)＝m有零点，求m的取值范围；
(2)确定m的取值范围，使得g(x)－f(x)＝0有两个相异实根．
(1) [2e，＋∞) (2) (－e2＋2e＋1，＋∞)
解：(1)∵g(x)＝x＋≥2
＝2e(x>0)，
当且仅当x＝时取等号．
∴当x＝e时，g(x)有最小值2e.
因此g(x)＝m有零点，只需m≥2e.
∴m∈[2e，＋∞)．
(2)若g(x)－f(x)＝0有两个相异实根，
则函数g(x)与f(x)的图像有两个不同的交点．
如图所示，作出函数g(x)＝x＋ (x>0)的大致图像．
∵f(x)＝－x2＋2ex＋m－1
＝－(x－e)2＋m－1＋e2，
∴其对称轴为x＝e，f(x)max＝m－1＋e2.
若函数f(x)与g(x)的图像有两个交点，
必须有m－1＋e2>2e，即m>－e2＋2e＋1.
即g(x)－f(x)＝0有两个相异实根，
则m的取值范围是(－e2＋2e＋1，＋∞)．
≥2＝2e(x>0)，当且仅当x＝
时取等号．∴当x＝e时，g(x)有最小值2e.
因此g(x)＝m有零点，只需m≥2e.
∴m∈[2e，＋∞)．
(2)若g(x)－f(x)＝0有两个相异实根，
则函数g(x)与f(x)的图像有两个不同的交点．
如图所示，作出函数g(x)＝x＋
(x>0)的大致图像．∵f(x)＝－x2＋2ex＋m－1
＝－(x－e)2＋m－1＋e2，
∴其对称轴为x＝e，f(x)max＝m－1＋e2.
若函数f(x)与g(x)的图像有两个交点，
必须有m－1＋e2>2e，即m>－e2＋2e＋1.
即g(x)－f(x)＝0有两个相异实根，
则m的取值范围是(－e2＋2e＋1，＋∞)．
练习册系列答案
相关题目
<-1.
,
),B(-1,3),C(2,3),则这个二次函数的解析式为__________.
内单调递减，求a的取值范围；
是奇函数，（其中
)
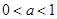时，讨论函数f(x)的增减性；
时，f(x)的值域是（1，
），求n与a的值。
小时
小时
函数f(x) =max{|x+1|，|x-2|}(x∈R)的最小值是（ ）
