题目内容
如图9,四边形ABCD中,AC、BD交于O,过O作AB的平行线,与AD、BC分别交于E、F,与CD的延长线交于K.求证:KO2=KE·KF.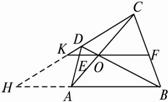
图9
思路分析:KO、KE、KF在一条直线上,要证明KO2=KE·KF,即要证
=
,显然要寻找中间比,现有图形无法将线段KO、KE、KF与平行线分线段成比例定理及其推论联系起来,若延长CK、BA,设它们交于H,则图形中出现两个基本图形.这就不难将
、
进行转换而找到中间比.
证明:延长CK、BA,设它们交于H.??
∵KO∥HB,?
∴
=
,
=
.?
∴
=
,即
=
.?
∵KF∥HB,同理可得
=
.?
∴
=
,即KO2=KE·KF.
练习册系列答案
星级口算天天练系列答案
相关题目
.
，NP 
…………………………8分
…………………………………9分
………………………………10分
为矩阵
属于λ的一个特征向量，求实数a，λ的值及A2。
（α为参数），曲线D的参数方程为
，（t为参数）。若曲线C、D有公共点，求实数m的取值范围。