题目内容
在△ABC 中,∠C =90°,∠B =30°,AC=1,M 为 AB 中点,将△ACM 沿 CM 折起,使 A、B 间的距离为  ,则 M 到面 ABC 的距离为( )
,则 M 到面 ABC 的距离为( )
(A)
(B)
(C)1
(D)
A
解析试题分析:由已知得AB=2,AM=MB=MC=1,BC= ,
,
由△AMC为等边三角形,取CM中点,则AD⊥CM,AD交BC于E,
则AD= ,DE=
,DE= ,CE=
,CE=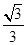 .
.
折起后,由BC2=AC2+AB2,知∠BAC=90°,
又cos∠ECA=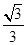 ,∴AE2=CA2+CE2-2CA•CEcos∠ECA=
,∴AE2=CA2+CE2-2CA•CEcos∠ECA= ,
,
于是AC2=AE2+CE2.∴∠AEC=90°.
∵AD2=AE2+ED2,∴AE⊥平面BCM,即AE是三棱锥A-BCM的高,AE= 。
。
设点M到面ABC的距离为h,∵S△BCM= ,∴由VA-BCM=VM-ABC,
,∴由VA-BCM=VM-ABC,
可得 ×
× =
=
 ×
× ×1×h,∴h=
×1×h,∴h= 。故选A.
。故选A.
考点:折叠问题,体积、距离的计算。
点评:中档题,折叠问题,要特别注意折叠前后“变”与“不变”的几何量。本题利用“等体积法”,确定了所求距离。

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
若直线a不平行于平面?,则下列结论成立的是( )
| A.内的所有直线都与直线a异面 |
| B.内不存在与a平行的直线 |
C. 内的直线都与a相交 内的直线都与a相交 |
D.直线a与平面 有公共点 有公共点 |
设 是两条不同的直线,
是两条不同的直线, 是两个不同的平面,有下列四个命题:
是两个不同的平面,有下列四个命题:
① 若 ; ② 若
; ② 若 ;
;
③ 若 ; ④ 若
; ④ 若
其中正确命题的序号是( )
| A.①③ | B.①② | C.③④ | D.②③ |
对于直线 ,
, 和平面
和平面 ,
, ,使
,使 成立的一个充分条件是( )
成立的一个充分条件是( )
A. , , ∥ ∥ | B. ∥ ∥ , , |
C. , , , , | D. , , , , |
设平面 与平面
与平面 相交于直线
相交于直线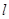 ,直线
,直线 在平面
在平面 内,直线
内,直线 在平面
在平面 内,且
内,且 ,则“
,则“ ”是“
”是“ ”的( )
”的( )
| A.充分不必要条件 | B.必要不充分条件 |
| C.充要条件 | D.既不充分也不必要条件 |
已知命题 ,
, 为直线,
为直线, 为平面,若
为平面,若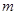 ∥
∥ ,
, ,则
,则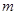 ∥
∥ ;命题
;命题 若
若 ,则
,则 ,则下列命题为真命题的是( )
,则下列命题为真命题的是( )
A. 或 或 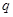 | B. 或 或 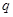 | C. 且 且 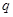 | D. 且 且 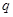 |
设m,n是两条不同的直线, 是三个不同的平 面,则下列为假命题的是
是三个不同的平 面,则下列为假命题的是
A.若 ,则 ,则 |
B.若 |
C.若 |
D.若 |
在空间,下列命题正确的是
| A.平行直线的平行投影重合 | B.平行于同一直线的两个平面平行 |
| C.垂直于同一平面的两个平面平行 | D.垂直于同一平面的两条直线平行 |
已知 是两条不同的直线,
是两条不同的直线, 是三个不同的平面,则下列命题中正确的是( )
是三个不同的平面,则下列命题中正确的是( )
A. ,则 ,则 | B. ,则 ,则 |
C. ,则 ,则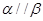 | D. ,则 ,则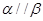 |