题目内容
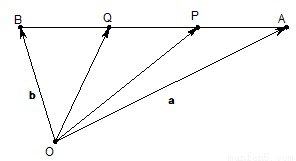
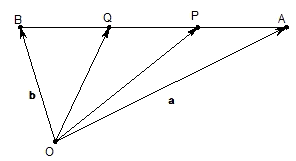 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若 ,
,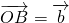 ,试用
,试用 ,
, 表示
表示 ,
,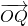 ,并判断
,并判断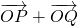 与
与 的关系;
的关系;
(2)受(1)的启示,如果点A1,A2,A3,…,An-1是AB的n(n≥3)等分点,你能得到什么结论?请证明你的结论.
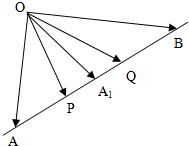 解:(1)如图:点P、Q是线段AB的三等分点
解:(1)如图:点P、Q是线段AB的三等分点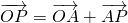 =
=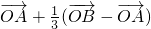 ,
,则
 ,同理
,同理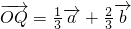 ,
,所以
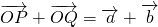
即:
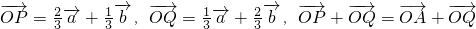 ,
,(2)设A1,A2.,…,An-1是AB的n等分点,
则
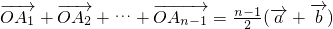 ;
;证:A1,A2,,An-1是线段n≥2的
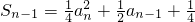 等分点,
等分点,先证明:
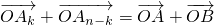 (1≤k≤n-1,n、k∈N+).
(1≤k≤n-1,n、k∈N+).由
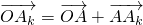 ,
, ,
,因为
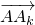 和
和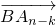 是相反向量,
是相反向量,则
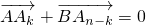 ,
,所以
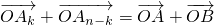 .
.记
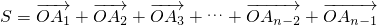 ,
,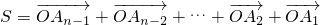
相加得

∴
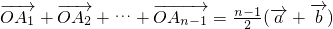 .
.分析:(1)由三角形法则及向量共线的数乘表示,分别用向量
 、
、 表示出
表示出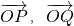 ,相加即得用向量
,相加即得用向量 、
、 表示
表示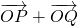 的表达式,进而判断
的表达式,进而判断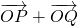 与
与 的关系;
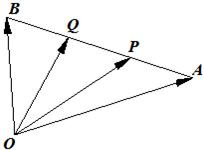
的关系;(2)受(1)的启示,如果点A1,A2,A3,…,An-1是AB的n(n≥3)等分点,归纳得出猜想
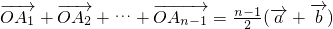 ,再数学归纳法证明结论.
,再数学归纳法证明结论.点评:本小题主要考查平行向量与共线向量、归纳推理、数学归纳法等基础知识,考查运算求解能力,考查化归与转化思想.属于中档题.

练习册系列答案
 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案
相关题目
 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若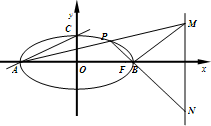 如图,设点P是椭圆
如图,设点P是椭圆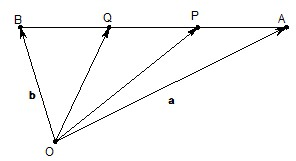 (1)如图,设点P,Q是线段AB的三等分点,若
(1)如图,设点P,Q是线段AB的三等分点,若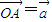 ,
,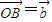 ,试用
,试用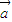 ,
,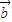 表示
表示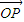 ,
,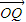 ,并判断
,并判断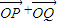 与
与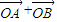 的关系;
的关系;