题目内容
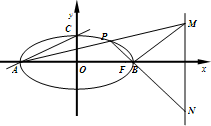 如图,设点P是椭圆E:
如图,设点P是椭圆E:| x2 |
| 4 |
(1)若椭圆E的右焦点为F,上顶点为C,求以F为圆心且与直线AC相切的圆的半径;
(2)设直线PA,PB分别交直线l:x=
| 10 |
| 3 |
分析:(1)先求出直线AC的方程,由直线与圆心相切的性质可知,圆心到直线的距离等于半径可求r
(2)要证明PN⊥BM,只要证明
•
=0,先设P的坐标,及直线AP,BP与直线x=
的交点M,N,由A,P,M三点共线可知AM,BM的斜率相等,AN,BN的斜率相等,结合点P在椭圆上,可寻求P,M,N的坐标的关系,代入即可证明
(2)要证明PN⊥BM,只要证明
| PN |
| BM |
| 10 |
| 3 |
解答:(1)解:由题意可知A(-2,0),B(2,0),C(0,1),F(
,0),
直线AC的方程为x-2y+2=0(2分)
设圆F的半径为r,则由以F为圆心的圆与直线AC相切可得圆心F到直线AC的距离为圆的半径r
∴r=
=
(5分)
(2)设P(x0,y0),直线AP,BP分别交直线x=
于M(
,y1),N(
,y2)两点
∵A,P,M三点共线
∴KAP=KAM即
=
,整理可得,y1=
(7分)
同理可得,
=
,整理可得,y2=
(9分)
∴y1y2=
∵P(x0,y0)在椭圆E:
+y2=1上
∴
+y02=1即可得y02=
(11分)
∴y1y2=
•
=
×
=-
(13分)
∴
•
=(
-x0,y2-y0)•(
-2,y1)=
(
-x0)+ (y2 -y0)y1
=
-
+y1y2-y1y0=
-
-
-
=
-
-
=
-
-
=0
∴PN⊥BM
| 3 |
直线AC的方程为x-2y+2=0(2分)
设圆F的半径为r,则由以F为圆心的圆与直线AC相切可得圆心F到直线AC的距离为圆的半径r
∴r=
|
| ||
|
| ||||
| 5 |
(2)设P(x0,y0),直线AP,BP分别交直线x=
| 10 |
| 3 |
| 10 |
| 3 |
| 10 |
| 3 |
∵A,P,M三点共线
∴KAP=KAM即
| y0 |
| x0+2 |
| y1 | ||
|
| 16y0 |
| 3(x0+2) |
同理可得,
| y2 | ||
|
| y0 |
| x0-2 |
| 4y0 |
| 3(x0-2) |
∴y1y2=
| 64y02 |
| 9(x02-4) |
∵P(x0,y0)在椭圆E:
| x2 |
| 4 |
∴
| x02 |
| 4 |
| 4-x02 |
| 4 |
∴y1y2=
| 64 |
| 9 |
| y02 |
| x02-4 |
| 64(4-x02) |
| 9(x02-4) |
| 1 |
| 4 |
| 16 |
| 9 |
∴
| PN |
| BM |
| 10 |
| 3 |
| 10 |
| 3 |
| 4 |
| 3 |
| 10 |
| 3 |
=
| 40 |
| 9 |
| 4x0 |
| 3 |
| 40 |
| 9 |
| 4x0 |
| 3 |
| 16 |
| 9 |
| 16y02 |
| 3(x0 +2) |
=
| 24 |
| 9 |
| 4x0 |
| 3 |
16•
| ||
| 3(x0+2) |
=
| 24 |
| 9 |
| 4x0 |
| 3 |
| 4(2+x0)(2-x0) |
| 3(x0+2) |
=0
∴PN⊥BM
点评:本题主要考查了点到直线的距离公司的应用,三点共线性质的应用,直线与圆的相交关系的应用,及向量的数量积的性质在证明几何关系中的应用,属于综合性试题

练习册系列答案
 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
 (2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且
(2012•芜湖二模)如图,直角坐标系XOY中,点F在x轴正半轴上,△OFG的面积为S.且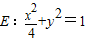 上的任意一点(异于左,右顶点A,B).
上的任意一点(异于左,右顶点A,B).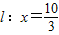 与点M,N,求证:PN⊥BM.
与点M,N,求证:PN⊥BM.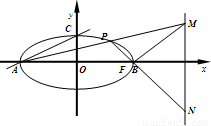
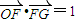 ,设
,设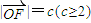 ,
,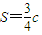 .
.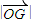 取最小值时,求椭圆E的标准方程.
取最小值时,求椭圆E的标准方程.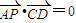 ,试求CD直线方程.
,试求CD直线方程.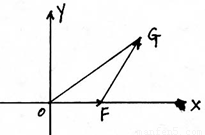
 上的任意一点(异于左,右顶点A,B).
上的任意一点(异于左,右顶点A,B). 与点M,N,求证:PN⊥BM.
与点M,N,求证:PN⊥BM.