题目内容
AB是某平面上一定线段，点P是该平面内的一动点，满足|
|-|
|=2，|
-
|=2
，则点P的轨迹是（ ）
| PA |
| PB |
| PA |
| PB |
| 5 |
| A、圆 | B、双曲线的一支 |
| C、椭圆的一部分 | D、抛物线 |
分析：根据|
|-|
|=2，|
-
|=2
可得|PA|-|PB|=2＜|AB|=2
即可根据双曲线的定义可得点P的轨迹是双曲线的一支．
| PA |
| PB |
| PA |
| PB |
| 5 |
| 5 |
解答：解：∵|
|-|
|=2
∴|PA|-|PB|=2
∵|
-
|=2
且
-
=
∴|AB|=2
∴|PA|-|PB|=2＜|AB|=2
即动点P到两定点A，B的距离之差小于两定点间的距离且|PA|＞|PB|
∴根据双曲线的定义可得点P的轨迹是双曲线的一支（靠近点B的一支）
故选B
| PA |
| PB |
∴|PA|-|PB|=2
∵|
| PA |
| PB |
| 5 |
| PA |
| PB |
| BA |
∴|AB|=2
| 5 |
∴|PA|-|PB|=2＜|AB|=2
| 5 |
∴根据双曲线的定义可得点P的轨迹是双曲线的一支（靠近点B的一支）
故选B
点评：此题主要考查求动点的轨迹．而求动点的轨迹不外乎直线，椭圆，双曲线，抛物线解题的关键是要利用题中的条件获得直线，椭圆，双曲线，抛物线的定义所满足的条件即可得解．
练习册系列答案
小学期末冲刺100分系列答案
期末复习检测系列答案
超能学典单元期中期末专题冲刺100分系列答案
黄冈360度定制密卷系列答案
相关题目
AB是某平面上一定线段且|AB|=3，点P是该平面内的一动点，满足|
|-|
=2，则点P的轨迹是（ ）
| PA |
| PB| |
| A、圆 | B、双曲线的一支 |
| C、椭圆的一部分 | D、抛物线 |
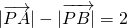，则点P的轨迹是
=2，|
|=
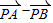，则点P的轨迹是（ ）