题目内容
若点 (p , q )在![]() ,
,![]() 中按均匀分布出现。
中按均匀分布出现。
(1)求方程![]() 有两个实数根的概率;
有两个实数根的概率;
(2) 若![]() ,p,q∈Z,试求方程
,p,q∈Z,试求方程![]()
当![]() 时恰有两个实根的概率。
时恰有两个实根的概率。
解:(1) ![]() ,
,![]() 表示一个正方形区域,易得其面积为36 ………(1分)
表示一个正方形区域,易得其面积为36 ………(1分)
若方程![]() 有两个实数根,则有
有两个实数根,则有![]() ,即
,即![]()
(注:若无等号扣1分)
解得表示正方形中圆以外的区域,其面积为36-![]() ,………………………(3分)
,………………………(3分)
即方程![]() 有两个实数根的概率为
有两个实数根的概率为![]() ……………………(4分)
……………………(4分)
要使得原方程有两个实根,则![]() 与
与![]() 的图像有且仅有2个交点,
的图像有且仅有2个交点,
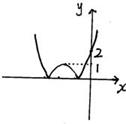
 所以
所以![]() =0或
=0或![]() >1
>1
又![]() 有 – 2.5 < p < - 0.5,所以p = -2 或 p = -1
有 – 2.5 < p < - 0.5,所以p = -2 或 p = -1
(i) 若![]() =0,则
=0,则![]() ,所以
,所以![]()
即![]() 解得q= 1或q = -2,故符合方程有两个实根的情况有
解得q= 1或q = -2,故符合方程有两个实根的情况有
(-2 ,1), (-2 , -2 ), ( -1 , 1),(-1 , -2)
共4种情况 。
(ii)若![]() >1,则
>1,则![]() ,所以
,所以![]()
即![]() ,∴q= -1 或q = 0,故符合方程有两个实根的情况
,∴q= -1 或q = 0,故符合方程有两个实根的情况
(-2 ,-1), (-2 , 0 ), ( -1 , -1),(-1 , 0)
有共4种情况;
综上所述,符合方程有两个实根的情况共有8种,
所以方程恰有两个实根的概率![]()
答:此方程恰有两个实根的概率为![]()

练习册系列答案
相关题目
 如图,点A、B为椭圆
如图,点A、B为椭圆