题目内容
阅读下面材料:根据两角和与差的正弦公式,有
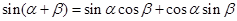 ------①
------①
 ------②
------②
由①+② 得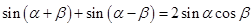 ------③
------③
令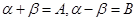 有
有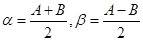
代入③得  .
.
(Ⅰ) 类比上述推理方法,根据两角和与差的余弦公式,证明:
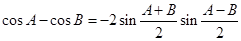 ;
;
(Ⅱ)若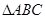 的三个内角
的三个内角 满足
满足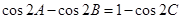 ,试判断
,试判断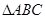 的形状.
的形状.
(提示:如果需要,也可以直接利用阅读材料及(Ⅰ)中的结论)
【答案】
(Ⅰ)见解析
(Ⅱ)勾股定理的逆定理知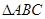 为直角三角形.
为直角三角形.
【解析】(1)写出两角和与差的余弦公式,两式相减,类比已知条件整理可证结论;
(2)根据二倍角的正弦公式把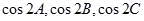 分别用
分别用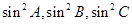 表示,再由正弦定理分别用
表示,再由正弦定理分别用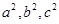 表示,已知条件可转化为
表示,已知条件可转化为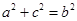 .所以
.所以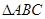 为直角三角形.也可以用(1)的结论化为角分析
为直角三角形.也可以用(1)的结论化为角分析
解法一:(Ⅰ)证明:因为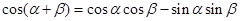 ,------①
,------①
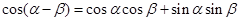 ,------②…………………1分
,------②…………………1分
①-② 得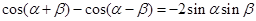 .------③……………………2分
.------③……………………2分
令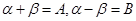 有
有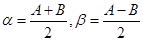 ,
,
代入③得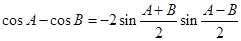 .………………………………5分
.………………………………5分
(Ⅱ)由二倍角公式,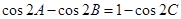 可化为
可化为
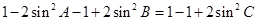 ,…………………………………8分
,…………………………………8分
所以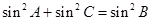 .…………………………………9分
.…………………………………9分
设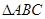 的三个内角A,B,C所对的边分别为
的三个内角A,B,C所对的边分别为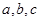 ,
,
由正弦定理可得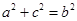 .………………………………11分
.………………………………11分
根据勾股定理的逆定理知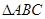 为直角三角形.…………………………………12分
为直角三角形.…………………………………12分
解法二:(Ⅰ)同解法一.
(Ⅱ)利用(Ⅰ)中的结论和二倍角公式,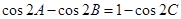 可化为
可化为
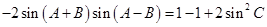 ,…………………………………8分
,…………………………………8分
因为A,B,C为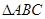 的内角,所以
的内角,所以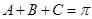 ,
,
所以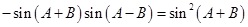 .
.
又因为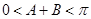 ,所以
,所以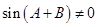 ,
,
所以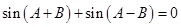 .
.
从而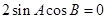 .……………………………………………9分
.……………………………………………9分
又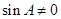 ,所以
,所以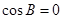 ,故
,故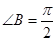 .……………………………………11分
.……………………………………11分
所以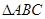 为直角三角形.
为直角三角形.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
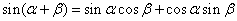 ----------①
----------①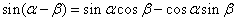 ------②
------②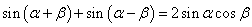 ------③
------③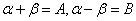 有
有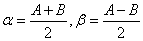
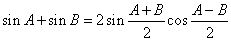 .
.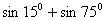 的值。
的值。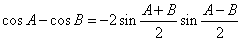 ;
;