题目内容
在平面直角坐标系xoy中,已知曲线C1:x2+y2=1,以平面直角坐标系xoy的原点O为极点,x轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线l:ρ(2cosθ-sinθ)=6.
(Ⅰ)将曲线C1上的所有点的横坐标,纵坐标分别伸长为原来的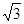 、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
、2倍后得到曲线C2,试写出直线l的直角坐标方程和曲线C2的参数方程.
(Ⅱ)在曲线C2上求一点P,使点P到直线l的距离最大,并求出此最大值.
:(Ⅰ)由题意知,直线l的直角坐标方程为:2x-y-6=0.
∵C2:(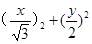 =1 ∴C2:的参数方程为:
=1 ∴C2:的参数方程为: (θ为参数)……5分
(θ为参数)……5分
(Ⅱ)设P(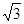 cosθ,2sinθ),则点P到l的距离为:
cosθ,2sinθ),则点P到l的距离为:
d= ,
,
∴当sin(60°-θ)=-1即点P(-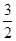 ,1)时,此时dwax=[
,1)时,此时dwax=[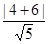 =2
=2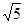
解析

练习册系列答案
相关题目
如图是某赛季甲、乙两名篮球运动员每场比赛得分的茎叶图,则甲、乙两人这几场比赛得分的中位数之和是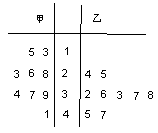
| A.62 | B.63 | C.64 | D.65 |
某小卖部销售一品牌饮料的零售价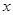 (元/评)与销售量
(元/评)与销售量 (瓶)的关系统计如下:
(瓶)的关系统计如下:
| 零售价x(元/瓶) | 3.0 | 3.2 | 3.4 | 3.6 | 3.8 | 4.0 |
| 销量y(瓶) | 50 | 44 | 43 | 40 | 35 | 28 |
已知的关系符合线性回归方程
 ,其中
,其中 .当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )
.当单价为4.2元时,估计该小卖部销售这种品牌饮料的销量为( )A.20 B.22 C.24 D.26
 中,曲线
中,曲线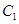 的参数方程为
的参数方程为 (
( 为参数),以坐标原点
为参数),以坐标原点 为极点,
为极点, 轴的非负半轴为极轴建立极坐标系,得曲线
轴的非负半轴为极轴建立极坐标系,得曲线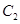 的极坐标方程为
的极坐标方程为 (
( )
)  :
:  (
( 为参数)过曲线
为参数)过曲线 轴负半轴的交点,求与直线
轴负半轴的交点,求与直线 .以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是:
.以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,直线l的参数方程是: (
( 是参数).
是参数). 参数方程转化为普通方程;
参数方程转化为普通方程; ,试求实数
,试求实数 值.
值. 被曲线
被曲线 所截得的弦长大于
所截得的弦长大于 ,求正整数
,求正整数 的最小值。
的最小值。 中,已知曲线
中,已知曲线 ,以平面直角坐标系
,以平面直角坐标系 为极点,
为极点, 轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线
轴的正半轴为极轴,取相同的单位长度建立极坐标系,已知直线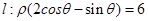 .
. 上的所有点的横坐标、纵坐标分别伸长为原来的
上的所有点的横坐标、纵坐标分别伸长为原来的 、
、 倍后得到曲线
倍后得到曲线 ,试写出直线的直角坐标方程和曲线
,试写出直线的直角坐标方程和曲线 ,使点
,使点



 ,从B口袋中摸出一个球是红球的概率为
,从B口袋中摸出一个球是红球的概率为 。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )
。现从两个口袋中各摸出一个球,那么这两个球中没有红球的概率是( )

