异面直线a与b垂直.c与a成30°角.则c与b的成角范围是[60°.90°]．题目和参考答案——青夏教育精英家教网—

题目内容

16．异面直线a与b垂直，c与a成30°角，则c与b的成角范围是[60°，90°]．

分析将异面直线所成的角转化为平面角，然后由题意，找出与直线a垂直的直线c，判定与b的夹角

解答解：如图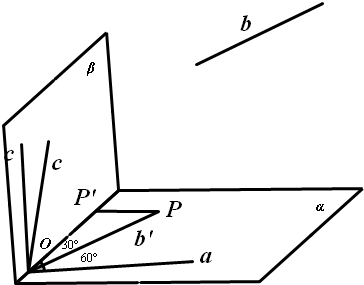
在α内做b的平行线b′，交a于O点，所有与a垂直的直线平移到O点组成一个与直线a垂直的平面β，O点是直线a与平面β的交点，
在直线b′上取一点P，做垂线PP'⊥平面β，交平面β于P'，∠POP'是b′与面β的夹角，为30°．
在平面β中，所有与OP'平行的线与b′的夹角都是30°．
在平面β所有与OP'垂直的线（由于PP'垂直于平面β，所以该线垂直与PP′，则该线垂直于平面α，所以该线与b'垂直），
与b'的夹角为90°，
与OP'夹角大于0°，小于90°的直线，与b'的夹角为锐角且大于30°．
故答案为：[60°，90°]

点评本题考查了异面直线所成的角，注意转化为平面角是解答问题的关键．

练习册系列答案

相关题目

6．

在极坐标系中，已知圆C的圆心在点C（2，0）且经过极点O，点P（6，0）．
（1）写出圆C的极坐标方程，过极点O作两条射线交圆C于A、B两点，A、B的极角分别为$\frac{π}{3}$，$\frac{π}{4}$，求|OA|+|OB|的值；
（2）设直角坐标系中x轴的正半轴与极轴重合，过点P作倾斜角为α（α为锐角）的直线l交圆C于M、N两点，若|PM|+|PN|=7，求cosα的值及M、N的直角坐标．

7．已知函数f（x）=x³+ax²+bx+c，过曲线y=f（x）上的点P（1，f（1））的切线方程为y=3x+1，y=f（x）在x=-2时有极值．
（1）求f（x）的表达式；
（2）求f（x）在[-3，1]上的单调区间和最大值．

4．

如图，在四棱锥P-ABCD中，底面ABCD是边长为2的正方形，侧面PCD⊥底面ABCD（1）若M，N分别为PC，BD的中点，求证：MN∥平面PAD；
（2）求证：平面PAD⊥平面PCD；
（3）若PD=CD=$\frac{\sqrt{2}}{2}PC$，求四棱锥P-ABCD的体积．

11．已知x＞0，求证：7-x-$\frac{9}{x}$≤1．

1．椭圆C：$\frac{x^2}{4}+\frac{y^2}{3}$=1的左、右顶点分别为A₁，A₂，点P在C上且直线PA₂的斜率的取值范围是[-2，-1]，那么直线PA₁斜率的取值范围是（　　）

$[{\frac{1}{2}，\frac{3}{4}}]$

D．

$[{\frac{3}{8}，\frac{3}{4}}]$

8．已知集合A={x|$\frac{2x+1}{x+2}$＜1，x∈R}，函数f（x）=|mx+1|（m∈R），函数g（x）=x²+ax+b（a，b∈R）的值域为[0，+∞）．
（1）若不等式f（x）≤3的解集为A，求m的值；
（2）在（1）的条件下，若|f（x）-2f（$\frac{x}{2}$）|≤k恒成立，求k的取值范围；
（3）若关于x的不等式g（x）＜c的解集为（m，m+6），求实数c的值．

5．

某市为了节约能源，拟出台“阶梯电价”制度，即制定住户月用电量的临界值a，若某住户某月用电量不超过a度，则按平价计费；若某月用电量超过a度，则超出部分按议价计费．未超出分布按平价计费．为确定a的值，随机调查了该市100户的月用电量，工作人员已将90户的用电量填在了下面的频率分布表中，最后10户的月用电量（单位：度）为：18 63 43 119 65 77 29 97 52 100

组别	月用电量	频数统计	频数	频率
1	[0，20）
2	[20，40）	正正一
3	[40，60）	正正正正
4	[60，80）	正正正正正
5	[80，100）	正正正正
6	[100，120）

（Ⅰ）完成频率分布表并绘制频率分布直方图；
（Ⅱ）根据已有信息，试估计全市住户的平均用电量（同一组数据用该区间的中点值作代表）；
（Ⅲ）若该市计划让全市75%的住户在“阶梯电价”出台前后缴纳的电费不变，试求临界值a．

6．求函数f（x）=2ln3x+8x的导函数．

试题分类