题目内容
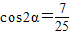 ,
,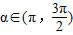 ,则
,则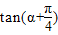 = .
= .
【答案】分析:根据α的范围,利用二倍角公式和已知条件求出cosα,可得sinα和tanα 的值,再利用两角和的正切公式求出 的值.
的值.
解答:解:∵ ,
,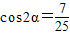 =2cos2α-1,可得 cosα=-
=2cos2α-1,可得 cosα=- ,∴
,∴
sinα=- ,tanα=
,tanα= .
.
∴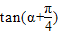 =
=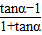 =
= ,
,
故答案为 .
.
点评:本题主要考查同角三角函数的基本关系,二倍角公式,两角和的正切公式的应用,属于中档题.
 的值.
的值.解答:解:∵
 ,
,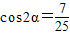 =2cos2α-1,可得 cosα=-
=2cos2α-1,可得 cosα=- ,∴
,∴sinα=-
 ,tanα=
,tanα= .
.∴
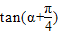 =
=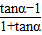 =
= ,
,故答案为
 .
.点评:本题主要考查同角三角函数的基本关系,二倍角公式,两角和的正切公式的应用,属于中档题.

练习册系列答案
相关题目
若ABCD是正方形,E是CD的中点,且
=
,
=
,则
=( )
| AB |
| a |
| AD |
| b |
| BE |
A、
| ||||||
B、
| ||||||
C、
| ||||||
D、
|