题目内容
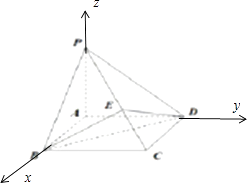
【题目】在四棱锥P﹣ABCD中,设底面ABCD是边长为1的正方形,PA⊥面ABCD. 
(1)求证:PC⊥BD;
(2)过BD且与直线PC垂直的平面与PC交于点E,当三棱锥E﹣BCD的体积最大时,求二面角E﹣BD﹣C的大小.
【答案】
(1)证明:∵四边形ABCD是正方形,∴BD⊥AC,PA⊥平面ABCD,
由此推出PA⊥BD,
又AC∩PA=A,
∴BD⊥平面PAC,而PC平面PAC,所以推出PC⊥BD
(2)解:设PA=x,三棱锥E﹣BCD的底面积为定值,求得它的高 ![]() ,
,
当 ![]() ,即
,即 ![]() 时,h最大值为
时,h最大值为 ![]() ,三棱锥E﹣BCD的体积达到最大值为
,三棱锥E﹣BCD的体积达到最大值为 ![]() .
.
以点A为坐标原点,AB为x轴,AD为y轴,PA为z轴建立空间直角坐标系,则 ![]() ,令E(x,y,z),
,令E(x,y,z), ![]() ,
, ![]() ,得
,得 ![]() ,∴
,∴ ![]() ,
,
设 ![]() 是平面EBD的一个法向量,
是平面EBD的一个法向量, ![]() ,
, ![]() ,
,
则 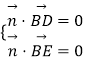 ,得
,得 ![]() .
.
又 ![]() 是平面BCD的一个法向量,
是平面BCD的一个法向量,
∴ 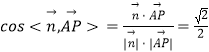 ,∴二面角E﹣BD﹣C为
,∴二面角E﹣BD﹣C为 ![]()
【解析】(1)证明BD⊥AC,PA⊥BD,即可证明BD⊥平面PAC,然后推出PC⊥BD.(2)设PA=x,三棱锥E﹣BCD的底面积为定值,求得它的高 ![]() ,求出三棱锥E﹣BCD的体积的最大值,以点A为坐标原点,AB为x轴,AD为y轴,PA为z轴建立空间直角坐标系,求出平面EBD的一个法向量,平面BCD的一个法向量,利用向量的数量积求解即可.
,求出三棱锥E﹣BCD的体积的最大值,以点A为坐标原点,AB为x轴,AD为y轴,PA为z轴建立空间直角坐标系,求出平面EBD的一个法向量,平面BCD的一个法向量,利用向量的数量积求解即可.
【考点精析】关于本题考查的直线与平面垂直的性质,需要了解垂直于同一个平面的两条直线平行才能得出正确答案.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目