Question

【题目】在平面直角坐标系中，将曲线(为参数) 上任意一点经过伸缩变换后得到曲线．以坐标原点为极点，轴的非负半轴为极轴，建立极坐标系，直线的极坐标方程为．

（1）求直线的普通方程和曲线的直角坐标方程；

（2）设直线与曲线交于两点，，求的值.

Answer 1

【答案】（1）的直角坐标方程为，的普通方程为；（2）

【解析】

（1）先求出曲线的参数方程，然后消去参数，即可求出曲线的直角坐标方程；由，，能求出直线的普通方程；

（2）求出直线的参数方程，并代入，得到，由此借助韦达定理即可求出的值.

（1）设曲线上任意一点，则有，

消去得，

所以，曲线的直角坐标方程为.

由，得的普通方程为.

（2）直线的参数方程为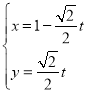(为参数)，将其代入，

得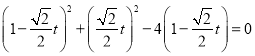，即，

设对应的参数分别为，则，

因为，

所以，.