题目内容
已知函数f(x)=
x3+
(a+2)x2+ax,x∈R,a∈R.
(Ⅰ)若f′(0)=-2,求函数f(x)的极值;
(Ⅱ)若函数f(x)在(1,2)上单调递增,求a的取值范围.
| 1 |
| 3 |
| 1 |
| 2 |
(Ⅰ)若f′(0)=-2,求函数f(x)的极值;
(Ⅱ)若函数f(x)在(1,2)上单调递增,求a的取值范围.
分析:(Ⅰ)先对函数f(x)求导,再令x=0,即可求出a的值;
(Ⅱ)函数f(x)在(1,2)上单调递增?f′(x)≥0在x∈(1,2)上恒成立?a≥-
在区间(1,2)上恒成立?a≥[-
]最大值,x∈(1,2),解出即可.
(Ⅱ)函数f(x)在(1,2)上单调递增?f′(x)≥0在x∈(1,2)上恒成立?a≥-
| x2+2x |
| x+1 |
| x2+2x |
| x+1 |
解答:解:(Ⅰ)∵f(x)=
x3+
(a+2)x2+ax,∴f′(x)=x2+(a+2)x+a.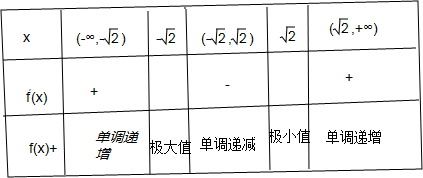
∵f′(0)=-2,∴a=-2.
∴f(x)=
x3-2x,f′(x)=x2-2.
令f′(x)=0,解得x=±
.
列表如下:
由表格可以看出:当x=-
时,f(x)极大值=f(-
)=
;
当x=
时,f(x)极小值=f(
)=-
.
(Ⅱ)∵函数f(x)在(1,2)上单调递增,
∴f′(x)=x2+(a+2)x+a≥0在区间(1,2)上恒成立.
亦即a≥-
在区间(1,2)上恒成立.
令g(x)=-
,则g′(x)=-
=-
<0,
∴函数g(x)在x∈(1,2)上为减函数,而函数g(x)在x=1时连续,
∴g(x)<g(1)=-
.
故a≥-
.
| 1 |
| 3 |
| 1 |
| 2 |

∵f′(0)=-2,∴a=-2.
∴f(x)=
| 1 |
| 3 |
令f′(x)=0,解得x=±
| 2 |
列表如下:
由表格可以看出:当x=-
| 2 |
| 2 |
| 4 |
| 3 |
| 2 |
当x=
| 2 |
| 2 |
| 4 |
| 3 |
| 2 |
(Ⅱ)∵函数f(x)在(1,2)上单调递增,
∴f′(x)=x2+(a+2)x+a≥0在区间(1,2)上恒成立.
亦即a≥-
| x2+2x |
| x+1 |
令g(x)=-
| x2+2x |
| x+1 |
| x2+2x+2 |
| (x+1)2 |
| (x+1)2+1 |
| (x+1)2 |
∴函数g(x)在x∈(1,2)上为减函数,而函数g(x)在x=1时连续,
∴g(x)<g(1)=-
| 3 |
| 2 |
故a≥-
| 3 |
| 2 |
点评:利用导数求函数的单调区间、极值、恒成立问题是最有效的方法之一,必须熟练掌握.

练习册系列答案
 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目