题目内容
.(12分)已知椭圆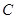 的中心在原点,
的中心在原点,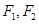 分别为它的左、右焦点,直线
分别为它的左、右焦点,直线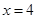 为它的一条准线,又知椭圆
为它的一条准线,又知椭圆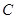 上存在点
上存在点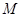 ,使得
,使得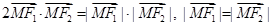 .
.
(1)求椭圆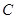 的方程;
的方程;
(2)若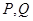 是椭圆
是椭圆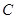 上不与椭圆顶点重合的任意两点,点
上不与椭圆顶点重合的任意两点,点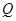 关于
关于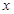 轴的对称点是
轴的对称点是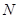 ,直线
,直线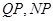 分别交
分别交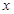 轴于点
轴于点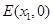 ,点
,点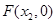 ,探究
,探究 是否为定值,若为定值,求出该定值,若不为定值,请说明理由.
是否为定值,若为定值,求出该定值,若不为定值,请说明理由.
【答案】
(1)设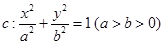 ∴
∴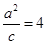 又
又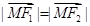 . ∴
. ∴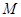 为短轴顶点.
为短轴顶点.
由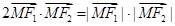 ∴
∴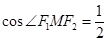 ∴
∴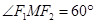 ,
,
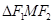 为等边三角形.
为等边三角形.
∴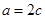 ∴
∴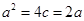 ∴
∴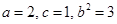 方程:
方程: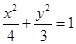
(2)令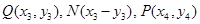
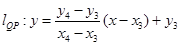 ,令
,令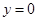 可得
可得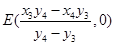
同理: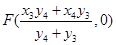 ∴
∴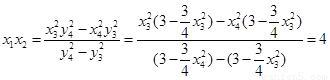 为定值
为定值
【解析】略

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
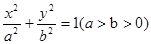 的左、右顶点的坐标分别为
的左、右顶点的坐标分别为 ,
, ,离心率
,离心率 。
。 ,
, ,若直线
,若直线 与椭圆交于
与椭圆交于 、
、 两点,证明直线
两点,证明直线 与直线
与直线 的交点在直线
的交点在直线 上。
上。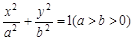 的离心率为
的离心率为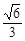 ,椭圆C上任意一点到椭圆两焦点的距离和为6.
,椭圆C上任意一点到椭圆两焦点的距离和为6.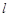 :
: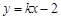 与椭圆C交于A,B两点,点P(0,1),且
与椭圆C交于A,B两点,点P(0,1),且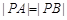 ,求直线
,求直线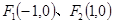 ,
, 为椭圆上一点,且
为椭圆上一点,且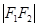 是
是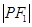 与
与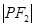 的等差中项.
的等差中项.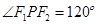 ,求
,求 的面积.
的面积.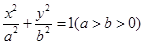 的离心率
的离心率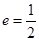 ,且原点
,且原点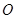 到直线
到直线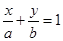 的距离为
的距离为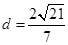 .
.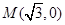 作直线与椭圆C交于
作直线与椭圆C交于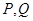 两点,求
两点,求 面积的最大值.
面积的最大值.